题目内容
9.若函数f(x)=x2-x+1,x∈[-1,1],不等式f(x)>2x+m恒成立,则m的取值范围是( )| A. | (-∞,-1) | B. | (-∞,3) | C. | (-1,3) | D. | (3,+∞) |
分析 根据不等式恒成立,利用参数分离法转化为求函数的最值问题,结合一元二次函数的最值性质进行求解即可.
解答 解:若f(x)>2x+m恒成立,
即x2-x+1>2x+m恒成立,
即x2-3x+1>m恒成立,
设g(x)=x2-3x+1,
则g(x)=(x-$\frac{3}{2}$)2-$\frac{5}{4}$,对称轴为x=$\frac{3}{2}$,
当x∈[-1,1]时,函数g(x)为减函数,
则当x=1时,函数取得最小值为g(1)=1-3+1=-1,
则m<-1,
故实数m的取值范围是(-∞,-1),
故选:A.
点评 本题主要考查函数恒成立问题,利用参数分离法,结合一元二次函数的最值性质是解决本题的关键.

练习册系列答案
相关题目
20.判断下面命题的真值“|x︳>0”( )
| A. | 假命题 | B. | 真命题 | C. | 不是命题 | D. | 可真可假 |
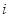 是虚数单位,
是虚数单位,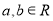 ,则“
,则“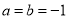 ”是“
”是“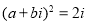 ”的( )
”的( )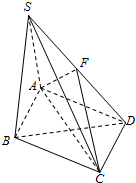 如图,在四棱锥S-ABCD中,底面ABCD是菱形,∠BAD=60°,侧面SAB⊥底面ABCD,并且SA=SB=AB=2,F为SD的中点.
如图,在四棱锥S-ABCD中,底面ABCD是菱形,∠BAD=60°,侧面SAB⊥底面ABCD,并且SA=SB=AB=2,F为SD的中点.