题目内容
7.设函数f(x)=$\left\{\begin{array}{l}{{3}^{x}+4a,x>3}\\{2x+{a}^{2},x≤3}\end{array}\right.$,其中a>0,若f(x)的值域为R,则实数a的取值范围是[7,+∞).分析 根据指数函数性质可知y=3x+4a,(x>3)是增函数,其值域y>27+4a,y=2x+a2(x≤3)也是增函数,其值域y≤9+a2.要使f(x)的值域为R,只需9+a2≥27+4a即可,从而可得实数a的取值范围.
解答 解:函数f(x)=$\left\{\begin{array}{l}{{3}^{x}+4a,x>3}\\{2x+{a}^{2},x≤3}\end{array}\right.$,其中a>0,
令y1=3x+4a,(x>3)是增函数,其值域y1>27+4a,
y2=2x+a2(x≤3)也是增函数,其值域y2≤9+a2.
要使f(x)的值域为R,只需9+a2≥27+4a
解得:a≥7或a≤-3.
∵a>0,
∴实数a的取值范围是[7,+∞)
故答案为:[7,+∞).
点评 本题考查了分段函数值域的问题,抓住分段函数中的各段函数的单调性,求出值域是关键.属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
16.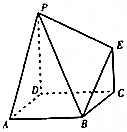 如图,多面体ABCDPE的底面ABCD是平行四边形,AD=AB=2,$\overrightarrow{AB}$•$\overrightarrow{AD}$=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2,则二面角A-PB-E的大小为( )
如图,多面体ABCDPE的底面ABCD是平行四边形,AD=AB=2,$\overrightarrow{AB}$•$\overrightarrow{AD}$=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2,则二面角A-PB-E的大小为( )
 如图,多面体ABCDPE的底面ABCD是平行四边形,AD=AB=2,$\overrightarrow{AB}$•$\overrightarrow{AD}$=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2,则二面角A-PB-E的大小为( )
如图,多面体ABCDPE的底面ABCD是平行四边形,AD=AB=2,$\overrightarrow{AB}$•$\overrightarrow{AD}$=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2,则二面角A-PB-E的大小为( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
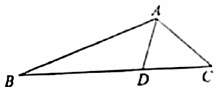 如图,已知AD是△ABC内角∠BAC的角平分线.
如图,已知AD是△ABC内角∠BAC的角平分线.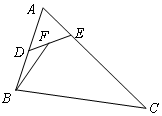 如图,在△ABC中,已知AB=2,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=5$\overrightarrow{AE}$,
如图,在△ABC中,已知AB=2,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=5$\overrightarrow{AE}$,