题目内容
化简
的结果是（ ）
| 1-2sin4cos4 |
| A、sin4+cos4 |
| B、sin4-cos4 |
| C、cos4-sin4 |
| D、-sin4-cos4 |
考点：同角三角函数基本关系的运用
专题：三角函数的图像与性质
分析：原式被开方数利用同角三角函数间的基本关系及二次根式的化简公式化简，在依据角的范围得到结果．
解答：
解：
=
=|sin 4-cos4|．
∵
＜4＜
，∴由三角函数线易知co 4＞sin4．
∴
=cos4-sin4．
故选：C．
| 1-2sin4cos4 |
| sin24-2sin4cos4+cos24 |
∵
| 5π |
| 4 |
| 3π |
| 2 |
∴
| 1-2sin4cos4 |
故选：C．
点评：此题考查了二倍角的正弦以及诱导公式的运用，熟练掌握公式是解题的关键，属于基础题．
练习册系列答案
相关题目
若点P在
的终边上，且|OP|=2（O为坐标原点），则点P的坐标（ ）
| 2π |
| 3 |
A、（1，
| ||
B、（
| ||
C、（-1，-
| ||
D、（-1，
|
某几何体的三视图如图，其正视图中的曲线部分为半个圆弧，则该几何体的表面积为（ ）
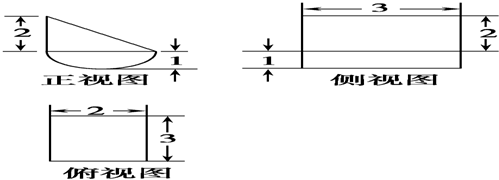
A、16+6
| ||
B、16+6
| ||
C、10+6
| ||
D、10+6
|