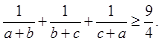题目内容
命题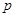 :关于
:关于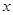 的不等式
的不等式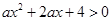 对一切
对一切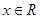 恒成立,命题
恒成立,命题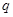 :函数
:函数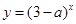 是增函数,若
是增函数,若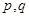 中有且只有一个为真命题,求实数
中有且只有一个为真命题,求实数 的取值范围.
的取值范围.
 .
.
解析试题分析:若不等式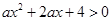 恒成立,则需对
恒成立,则需对 的取值情况进行分类讨论,若
的取值情况进行分类讨论,若 ,显然成立,过
,显然成立,过 ,根据一元二次不等式的相关知识点,可知问题等价于
,根据一元二次不等式的相关知识点,可知问题等价于 ,综合考虑易得命题
,综合考虑易得命题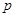 等价于
等价于 ,对于函数
,对于函数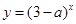 ,若其为增函数,只需
,若其为增函数,只需 ,从而
,从而 ,根据条件中
,根据条件中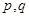 中有且只有一个为真命题,需分以下两种情况分类讨论:
中有且只有一个为真命题,需分以下两种情况分类讨论: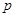 真
真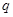 假,
假,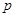 假
假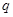 真,从而可以得到实数
真,从而可以得到实数 的取值范围是
的取值范围是 .
.
试题解析:若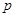 成立:当
成立:当 时成立,
时成立,
当 时,
时, ,∴
,∴ ,
,
若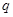 成立:
成立: ,
,
∵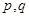 中有且只有一个为真命题,∴
中有且只有一个为真命题,∴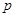 真
真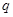 假或
假或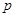 假
假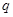 真,
真,
若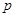 真
真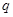 假:
假: ,若
,若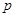 假
假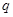 真,则
真,则 ,
,
∴满足条件的 的取值范围为
的取值范围为 .
.
考点:1.一元二次不等式;2.指数函数的单调性.

练习册系列答案
相关题目
 的解集为________.
的解集为________.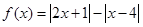
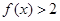 ;
; 的最小值.
的最小值. 的不等式
的不等式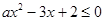 的解集为
的解集为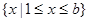 .
.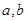 的值;
的值;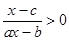 (
(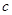 为常数).
为常数).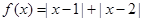
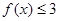 的解集;
的解集;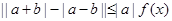 (
(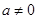 ,
,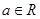 ,
,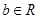 )恒成立,求实数
)恒成立,求实数 的范围.
的范围.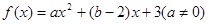 .
.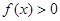 的解集为
的解集为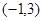 .求
.求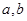 的值;
的值;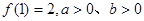 求
求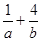 的最小值.
的最小值.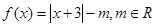 ,且
,且 的解集为
的解集为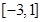 .
.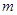 的值;
的值;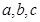 都是正数,且
都是正数,且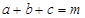 ,求证:
,求证: