题目内容
设函数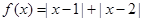
(1)求不等式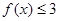 的解集;
的解集;
(2)若不等式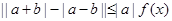 (
(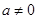 ,
,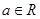 ,
,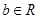 )恒成立,求实数
)恒成立,求实数 的范围.
的范围.
(1) ;(2)
;(2) .
.
解析试题分析:(1)欲解不等式,需去掉绝对值,考虑到含有两个绝对值,因此分三段去,然后解.(2)要使不等式恒成立,则 ,考虑到不等式性质
,考虑到不等式性质 ,不等式右侧可化简.
,不等式右侧可化简.
试题解析:
去绝对值,函数可化为 ,分三段解不等式
,分三段解不等式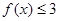 ,可得解集为:
,可得解集为: .
.
由 , 可得
, 可得 , 由(1)可解得:
, 由(1)可解得:
考点:(1)含绝对不等会的解法;(2)恒成立问题(一般采用分离常数).

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 .
.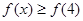 的解集;
的解集;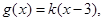
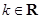 ,若
,若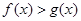 对任意的
对任意的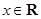 都成立,求
都成立,求 的取值范围.
的取值范围.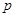 :关于
:关于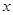 的不等式
的不等式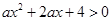 对一切
对一切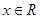 恒成立,命题
恒成立,命题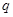 :函数
:函数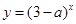 是增函数,若
是增函数,若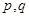 中有且只有一个为真命题,求实数
中有且只有一个为真命题,求实数 的取值范围.
的取值范围.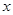 的不等式
的不等式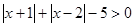 .
.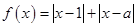 .
. 时,解不等式
时,解不等式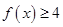 ;
;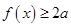 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.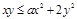 对于
对于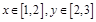 恒成立,求
恒成立,求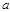 的取值范围”提出了各自的解题思路. 甲说:“可视
的取值范围”提出了各自的解题思路. 甲说:“可视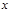 为变量,
为变量,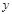 为常量来分析”; 乙说:“不等式两边同除以
为常量来分析”; 乙说:“不等式两边同除以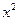 >|x-a| 至少有一个负数解,则实数a的取值范围是 .
>|x-a| 至少有一个负数解,则实数a的取值范围是 .