题目内容
设函数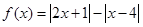
(1)解不等式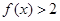 ;
;
(2)求函数 的最小值.
的最小值.
(1) ;(2)
;(2)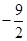 .
.
解析试题分析:(1)解含绝对值的不等式,关键是去掉绝对值符号,其方法有三种:①定义法;②平方法;③分区间讨论法,这里用的是分区间讨论法,遇到多个绝对值时常用此方法;(2)求绝对值函数的值域,通常是通过分区间讨论,去掉绝对值符号,将绝对值函数改写成分段函数,然后就每段求 的范围,最后再将每段求得的范围求并集,注意不是求交集,从而得到绝对值函数的值域.
的范围,最后再将每段求得的范围求并集,注意不是求交集,从而得到绝对值函数的值域.
试题解析:(1)不等式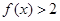 等价于:
等价于:
① ;
;
② ;
;
③ ,
,
综合①②③得不等式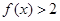 的解集为:
的解集为:
(2)①当 时,
时,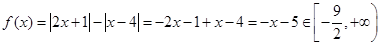 ;
;
②当 时,
时,
③当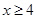 时,
时,
综合①②③得函数 的值域为
的值域为 ,因此求函数
,因此求函数 的最小值为
的最小值为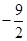 .
.
考点:1.含绝对值的不等式的解法;2.绝对值函数的值域的求法;3.分类讨论思想.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 对于一切
对于一切 恒成立,则
恒成立,则 的取值范围是___________
的取值范围是___________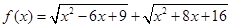 .
.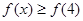 的解集;
的解集;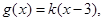
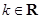 ,若
,若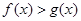 对任意的
对任意的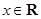 都成立,求
都成立,求 的取值范围.
的取值范围.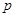 :关于
:关于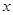 的不等式
的不等式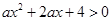 对一切
对一切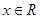 恒成立,命题
恒成立,命题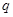 :函数
:函数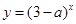 是增函数,若
是增函数,若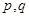 中有且只有一个为真命题,求实数
中有且只有一个为真命题,求实数 的取值范围.
的取值范围.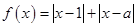 .
. 时,解不等式
时,解不等式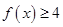 ;
;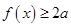 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.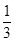 ,|2x-y|<
,|2x-y|<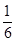 ,求证:|y|<
,求证:|y|<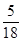 .
.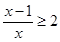 的解集为______________
的解集为______________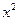 >|x-a| 至少有一个负数解,则实数a的取值范围是 .
>|x-a| 至少有一个负数解,则实数a的取值范围是 . 的解为 。
的解为 。