题目内容
设函数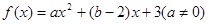 .
.
(1)若不等式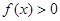 的解集为
的解集为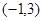 .求
.求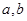 的值;
的值;
(2)若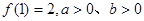 求
求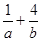 的最小值.
的最小值.
(1)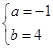 ;(2)
;(2) 的最小值为9.
的最小值为9.
解析试题分析:(1)先根据不等式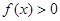 的解集为
的解集为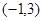 得出
得出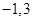 是方程
是方程 的两个根,进而根据二次方程根与系数的关系得到
的两个根,进而根据二次方程根与系数的关系得到 ,从中求解方程组即可;(2)先由条件
,从中求解方程组即可;(2)先由条件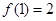 得出
得出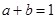 ,进而将
,进而将 变形为
变形为 ,应用基本不等式即可求出它的最小值,注意关注基本不等式的三个条件:一正、二定、三相等.
,应用基本不等式即可求出它的最小值,注意关注基本不等式的三个条件:一正、二定、三相等.
试题解析:(1)根据题意,由于函数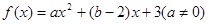
且不等式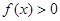 的解集
的解集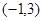 ,则说明
,则说明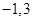 是方程
是方程 的两个根,那么二次方程根与系数的关系可得
的两个根,那么二次方程根与系数的关系可得
(2)由于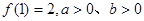 ,则可知
,则可知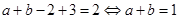
所以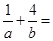

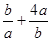
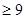
当且仅当 且
且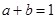 即
即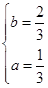 时成立,所以
时成立,所以 的最小值为9.
的最小值为9.
考点:1.二次不等式;2.基本不等式的应用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
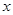 的不等式
的不等式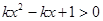 恒成立,则实数k的取值范围是__________________.
恒成立,则实数k的取值范围是__________________.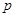 :关于
:关于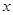 的不等式
的不等式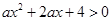 对一切
对一切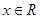 恒成立,命题
恒成立,命题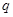 :函数
:函数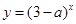 是增函数,若
是增函数,若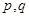 中有且只有一个为真命题,求实数
中有且只有一个为真命题,求实数 的取值范围.
的取值范围.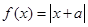 .
.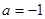 时,求不等式
时,求不等式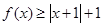 的解集;
的解集;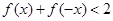 存在实数解,求实数
存在实数解,求实数 的取值范围.
的取值范围.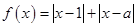 .
. 时,解不等式
时,解不等式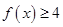 ;
;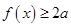 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.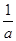 ,比较f(x)与m的大小.
,比较f(x)与m的大小.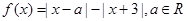 .
.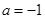 时,解不等式
时,解不等式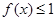 ;
;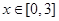 时,
时,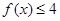 ,求a的取值范围.
,求a的取值范围.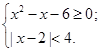
 的解为 。
的解为 。