题目内容
已知函数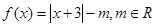 ,且
,且 的解集为
的解集为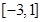 .
.
(1)求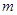 的值;
的值;
(2)已知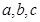 都是正数,且
都是正数,且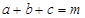 ,求证:
,求证: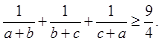
(1)2;(2)参考解析
解析试题分析:(1)含绝对值的不等式的解法主要通过两种方法解决,一是利用绝对值的几何意义,其二是通过平方来处理.由于函数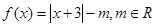 ,且
,且 的解集为
的解集为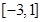 ,所以可得
,所以可得 .即
.即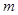 的值.本小题另外用三项的均值不等式来证明.
的值.本小题另外用三项的均值不等式来证明.
(2)通过(1)可得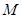 的值,根据题意利用
的值,根据题意利用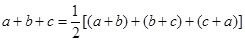 通过柯西不等式可证得结论.
通过柯西不等式可证得结论.
试题解析:(1) 方法一: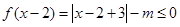 ,
, ,
,
所以 ,且
,且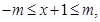 所以
所以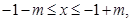 又不等式的解集为
又不等式的解集为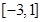 ,故
,故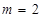 ;
;
方法二: 即:
即: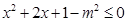 ,且
,且 ,
,
不等式的解集为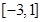 ,所以方程
,所以方程 的两个根为
的两个根为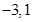 ,
,
故 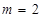 ;
;
(2) 证明一: 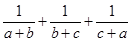
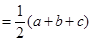
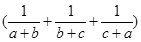


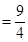 ,当且仅当
,当且仅当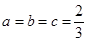 时,等号成立.
时,等号成立.
证明二: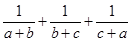
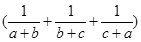
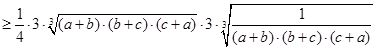
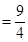 ,当且仅当
,当且仅当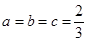 时,等号成立.
时,等号成立.
考点:1.绝对值不等式.2.柯西不等式.

练习册系列答案
相关题目
 :关于
:关于 的不等式
的不等式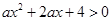 对一切
对一切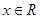 恒成立,命题
恒成立,命题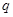 :函数
:函数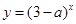 是增函数,若
是增函数,若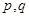 中有且只有一个为真命题,求实数
中有且只有一个为真命题,求实数 的取值范围.
的取值范围.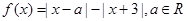 .
.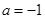 时,解不等式
时,解不等式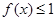 ;
;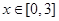 时,
时,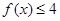 ,求a的取值范围.
,求a的取值范围.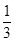 ,|2x-y|<
,|2x-y|<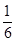 ,求证:|y|<
,求证:|y|<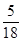 .
.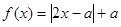 .
.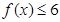 的解集为
的解集为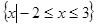 ,求实数a的值;
,求实数a的值; 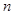 使
使 成立,求实数
成立,求实数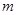 的取值范围.
的取值范围. 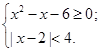

 的解集;
的解集;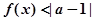 的解集非空,求实数
的解集非空,求实数 的取值范围.
的取值范围.