题目内容
(本小题满分13分)已知椭圆的焦点在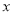 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线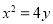 的焦点,离心率
的焦点,离心率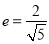 .
.
(1)求椭圆的标准方程;
(2)过椭圆的右焦点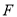 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线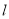 ,交椭圆于
,交椭圆于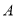 、
、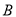 两点,设点
两点,设点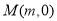 是线段
是线段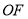 上的一个动点,且
上的一个动点,且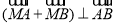 ,求
,求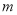 的取值范围;
的取值范围;
(3)设点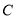 是点
是点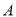 关于
关于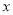 轴的对称点,在
轴的对称点,在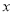 轴上是否存在一个定点
轴上是否存在一个定点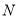 ,使得
,使得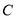 、
、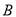 、
、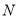 三点共线?若存在,求出定点
三点共线?若存在,求出定点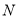 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(1)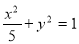 ,(2)
,(2)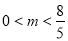 ,(3)存在定点
,(3)存在定点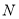
【解析】
试题分析:首先根据条件求出椭圆的方程,第二步直线过右焦点可设出直线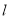 的方程,代入椭圆的方程,消去
的方程,代入椭圆的方程,消去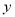 得出关于
得出关于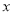 的一元二次方程,设而不求,利用根与系数关系写出
的一元二次方程,设而不求,利用根与系数关系写出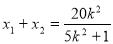 ,
,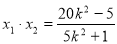
,再利用点在直线上求出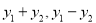 ,最后利用向量的坐标运算,根据
,最后利用向量的坐标运算,根据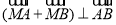 得:
得: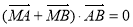 ,得出等式
,得出等式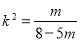 ,由于
,由于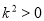 ,可得
,可得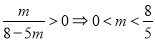 ,第三步假设在
,第三步假设在 轴上存在定点
轴上存在定点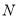 ,使得
,使得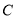 、
、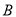 、
、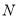 三点共线.依题意
三点共线.依题意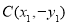 ,写出直线
,写出直线 的方程,与
的方程,与 轴的交点可令
轴的交点可令 ,求出点
,求出点 的横坐标,又点
的横坐标,又点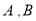 在直线
在直线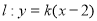 上, ∴
上, ∴ 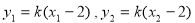 ,代入减元可得
,代入减元可得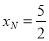 ,所以过
,所以过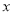 轴上一个定点
轴上一个定点 .
.
试题解析:(1)设椭圆方程为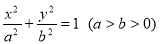 ,由题意
,由题意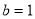 ,又
,又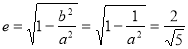 ,
,
∴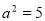 ,故椭圆方程为
,故椭圆方程为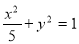 .
.
由(1)得右焦点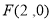 ,则
,则 ,设
,设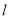 的方程为
的方程为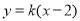 (
(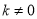 )代入
)代入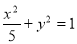
得,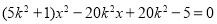 ,∴
,∴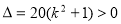 ,
,
设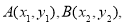 则
则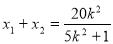 ,
,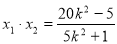 , 且
, 且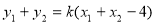 ,
, 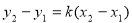 .
.
∴ 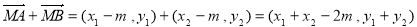 ,
,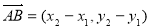 ,
,
由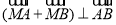 ,得
,得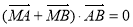 ,
,
即: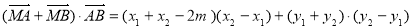
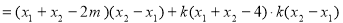
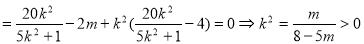
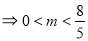 ,
,
∴ 当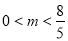 时,有
时,有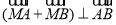 成立.
成立.
在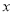 轴上存在定点
轴上存在定点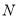 ,使得
,使得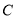 、
、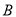 、
、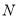 三点共线.依题意
三点共线.依题意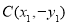 ,直线
,直线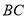 的方程为
的方程为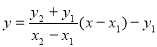 ,令
,令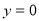 ,则
,则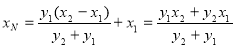 ,点
,点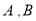 在直线
在直线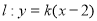 上, ∴
上, ∴ 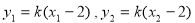 ,
,
∴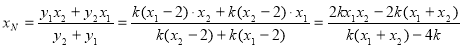
 ,∴ 在
,∴ 在 轴上存在定点
轴上存在定点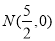 ,使得
,使得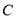 、
、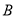 、
、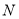 三点共线.
三点共线.
考点:1.设而不求思想;2.解析几何问题向量运算综合;3.存在性命题的解题方法;

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
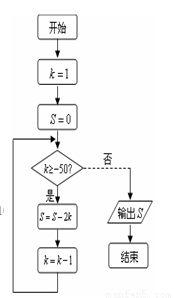
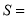 ( )
( )
 且
且 ,则
,则 从小到大的顺序是___________.
从小到大的顺序是___________. 是定义在
是定义在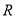 上的偶函数,且
上的偶函数,且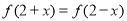 ,当
,当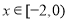 时,
时,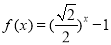 ,若函数
,若函数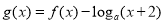
 且
且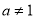 )在区间
)在区间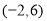 内恰有4个零点,则实数
内恰有4个零点,则实数 的取值范围是( )
的取值范围是( ) B.
B.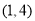 C.
C.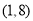 D.
D.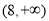
 上的函数
上的函数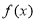 满足
满足 ,当
,当 时,
时,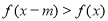 ,则不等式
,则不等式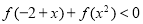 的解集为( )
的解集为( )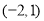 B.
B.
 D.
D.
 ,底面
,底面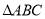 中,
中, ,
, ,棱
,棱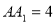 ,
, 分别是
分别是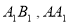 的中点.
的中点.
 的值;
的值; 与平面
与平面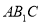 所成的角的正弦值.
所成的角的正弦值. 的图像如图所示,
的图像如图所示, 的导函数,则下列数值排序正确的( )
的导函数,则下列数值排序正确的( )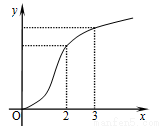



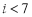 B.
B.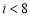 C.
C.  D.
D.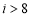
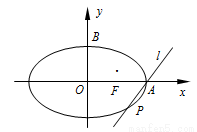
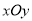 中,椭圆
中,椭圆 的右准线方程为
的右准线方程为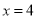 ,右顶点为
,右顶点为 ,
,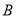 ,右焦点为
,右焦点为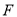 ,斜率为
,斜率为 的直线
的直线 经过点
经过点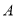 ,且点
,且点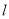 的距离为
的距离为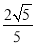 .
.
 的标准方程;
的标准方程; 绕点
绕点 旋转,它与椭圆
旋转,它与椭圆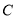 相交于另一点
相交于另一点 ,当
,当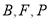 三点共线时,试确定直线
三点共线时,试确定直线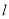 的斜率.
的斜率.