题目内容
(本小题满分12分)如图,直三棱柱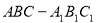 ,底面
,底面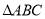 中,
中, ,
, ,棱
,棱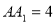 ,
, 分别是
分别是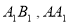 的中点.
的中点.

(1) 求 的值;
的值;
(2) 求直线 与平面
与平面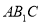 所成的角的正弦值.
所成的角的正弦值.
(1) ,(2)
,(2) ,
,
【解析】
试题分析:由已知 ,
, ,满足
,满足 ,即
,即 ,∴ 以
,∴ 以 为原点,分别以
为原点,分别以 所在直线为
所在直线为 轴建立如图的空间直角坐标系
轴建立如图的空间直角坐标系 ,写出相关点的坐标,求出
,写出相关点的坐标,求出 ,第二步先写出向量
,第二步先写出向量 的坐标,再求出平面
的坐标,再求出平面 的法向量,最后利用线面角公式,利用空间向量运算求出线面角的正弦值;
的法向量,最后利用线面角公式,利用空间向量运算求出线面角的正弦值;
试题解析:(1)由 ,
, ,得
,得 ,即
,即 ∴ 以
∴ 以 为原点,分别以
为原点,分别以 所在直线为
所在直线为 轴建立如图的空间直角坐标系
轴建立如图的空间直角坐标系 ,则
,则 ,∴
,∴  ,
, ,有
,有 .
.
(2) ,
, ,
, ,
, ,
,
设平面 的法向量
的法向量 ,
,
则 ,取
,取 .
.
设直线 与平面
与平面 所成的角为
所成的角为 ,
,
∴ ,故直线
,故直线 与平面
与平面 所成的角的正弦值是
所成的角的正弦值是 .
.
考点:利用空间向量求线面角;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,则下列不等式中恒成立的是 ( )
,则下列不等式中恒成立的是 ( ) B.
B. C.
C. D.
D.

 ,且满足
,且满足 ,则
,则 值( )
值( )  B.-
B.- D.
D.
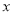 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线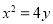 的焦点,离心率
的焦点,离心率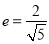 .
.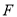 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线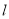 ,交椭圆于
,交椭圆于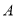 、
、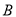 两点,设点
两点,设点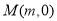 是线段
是线段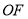 上的一个动点,且
上的一个动点,且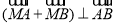 ,求
,求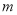 的取值范围;
的取值范围;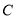 是点
是点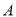 关于
关于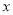 轴的对称点,在
轴的对称点,在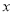 轴上是否存在一个定点
轴上是否存在一个定点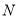 ,使得
,使得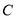 、
、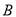 、
、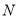 三点共线?若存在,求出定点
三点共线?若存在,求出定点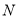 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.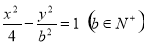 的两个焦点为
的两个焦点为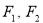 ,
, 为坐标原点,点
为坐标原点,点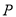 在双曲线上,且
在双曲线上,且 ,若
,若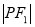 、
、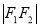 、
、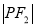 成等比数列,则
成等比数列,则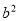 等于( )
等于( ) 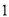 B.
B.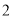 C.
C. D.
D.
 ( )
( ) 
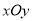 中,设直线
中,设直线 与圆
与圆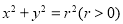 交于
交于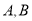 两点,
两点,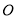 为坐标原点,若圆上一点
为坐标原点,若圆上一点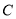 满足
满足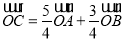 ,则
,则 .
.