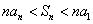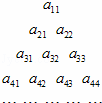题目内容
对于函数 和
和 ,若存在常数
,若存在常数 ,对于任意
,对于任意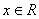 ,不等式
,不等式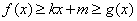 都成立,则称直线
都成立,则称直线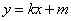 是函数
是函数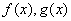 的分界线. 已知函数
的分界线. 已知函数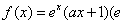 为自然对数的底,
为自然对数的底, 为常数).
为常数).
(Ⅰ)讨论函数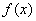 的单调性;(Ⅱ)设
的单调性;(Ⅱ)设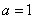 ,试探究函数
,试探究函数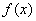 与函数
与函数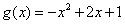 是否存在“分界线”?若存在,求出分界线方程;若不存在,试说明理由.
是否存在“分界线”?若存在,求出分界线方程;若不存在,试说明理由.
解:(1) , 当
, 当 时,
时, ,即
,即 ,
,
函数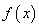 在区间
在区间 上是增函数,在区间
上是增函数,在区间 上是减函数;当
上是减函数;当 时,
时, ,函数
,函数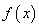 是区间
是区间 上的增函数 当
上的增函数 当 时,
时, 即
即 ,
,
函数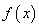 在区间
在区间 上是增函数,在区间
上是增函数,在区间 上是减函数.
上是减函数.
(2)若存在,则 恒成立,令
恒成立,令 ,则
,则 ,所以
,所以 , 因此:
, 因此: 恒成立,即
恒成立,即 恒成立,由
恒成立,由 得到:
得到: ,
,
现在只要判断 是否恒成立,设
是否恒成立,设 ,因为:
,因为: ,
,
当 时,
时, ,
, ,当
,当 时,
时, ,
, ,所以
,所以 ,即
,即 恒成立,所以函数
恒成立,所以函数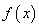 与函数
与函数 存在“分界线”.
存在“分界线”.

练习册系列答案
相关题目

 ,则P⊙Q= ( )
,则P⊙Q= ( ) B
B  C [1,2] D (2,+
C [1,2] D (2,+ )
)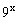
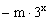 +m+1对x∈(0,
+m+1对x∈(0,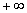 )的图象恒在x轴上方,则m的取值范围是 ( )
)的图象恒在x轴上方,则m的取值范围是 ( )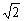 <m<2+2
<m<2+2 满足
满足
 满足
满足 ,则
,则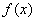 满足对
满足对 ,且
,且 ,都有
,都有 ,则
,则 的元素个数为 .
的元素个数为 .  (Ⅰ)求函数的定义域,并证明
(Ⅰ)求函数的定义域,并证明
 恒成立,求实数
恒成立,求实数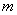 的取值范围;
的取值范围; 时,试比较
时,试比较 与
与 的大小关系.
的大小关系.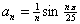 ,
,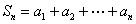 . 在
. 在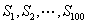 中,正数的个数是 ( )
中,正数的个数是 ( )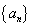 的前
的前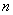 项和
项和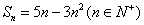 ,则当
,则当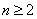 时,有( )
时,有( )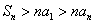 (B)
(B)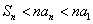 (C)
(C)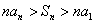 (D)
(D)