题目内容
14. 四棱锥P-ABCD中,PA⊥平面ABCD,PA=4PQ=4,底面为直角梯形∠CDA=∠BAD=90°,AB=2,CD=1,AD=$\sqrt{2}$,M,N分别是PD,PB的中点.
四棱锥P-ABCD中,PA⊥平面ABCD,PA=4PQ=4,底面为直角梯形∠CDA=∠BAD=90°,AB=2,CD=1,AD=$\sqrt{2}$,M,N分别是PD,PB的中点.(Ⅰ)求证:MQ∥平面PCB;
(Ⅱ)求截面MCN与底面ABCD所成二面角的大小.
分析 (1)取AP的中点E,连结ED,则ED∥CN证明MQ∥CN,然后证明MQ∥平面PCB.
(2)以A为原点,以AD,AB,AP分别为x,y,z建立空间直角坐标系O-xyz,求出平面的MCN的法向量,又$\overrightarrow{AP}=({0,0,4})$为平面ABCD的法向量,利用空间向量的数量积求解截面MCN与底面ABCD所成二面角的大小为$\frac{π}{3}$.
解答 解:(1)取AP的中点E,连结ED,则ED∥CN,…1分依题有Q为EP的中点,所以MQ∥ED,所以MQ∥CN,…2分
又MQ?平面PCB,CN?平面PCB,∴MQ∥平面PCB…4分
(2)以A为原点,以AD,AB,AP分别为x,y,z建立空间直角坐标系O-xyz,
设平面的MCN的法向量为$\overrightarrow n=({x,y,z})$,又$\overrightarrow{CM}=({-\frac{{\sqrt{2}}}{2},-1,2}),\overrightarrow{CN}=({-\sqrt{2},0,2})$
则有:$\left\{\begin{array}{l}\overrightarrow n⊥\overrightarrow{CM}⇒({x,y,z})•({-\frac{{\sqrt{2}}}{2},-1,2})=0⇒-\frac{{\sqrt{2}}}{2}x-y+2z=0\\ \overrightarrow n⊥\overrightarrow{CN}⇒({x,y,z})•({-\sqrt{2},0,2})=0⇒-\sqrt{2}x+2z=0\end{array}\right.$
令z=1,则$x=\sqrt{2},y=1⇒\overrightarrow n=({\sqrt{2},1,1})$,…6分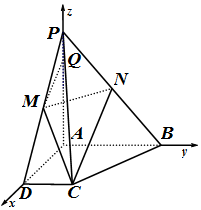
又$\overrightarrow{AP}=({0,0,4})$为平面ABCD的法向量,
∴$cos\left?{\overrightarrow n,\overrightarrow{AP}}\right>=\frac{{\overrightarrow n•\overrightarrow{AP}}}{{|{\overrightarrow n}|•|{\overrightarrow{AP}}|}}=\frac{4}{2×4}=\frac{1}{2}$,
又截面MCN与底面ABCD所成二面角为锐二面角,
∴截面MCN与底面ABCD所成二面角的大小为$\frac{π}{3}$…8分.
点评 本题考查空间向量的数量积求解二面角的平面角的大小,直线与平面平行的判断,考查空间想象能力以及计算能力逻辑推理能力.

| A. | 2 | B. | 3 | C. | 4 | D. | 无数个 |
| A. | 30人,30人,30人 | B. | 30人,45人,15人 | C. | 20人,30人,10人 | D. | 10人,15人,5人 |
| A. | {2,3,4} | B. | {2,3,6} | C. | {2,3,4,6} | D. | {3,4,6} |
 若f′(x)为定义在R上的函数f(x)的导函数,且y=3f′(x)的图象如图所示,则y=f(x)的单调递增开区间是(-∞,3).
若f′(x)为定义在R上的函数f(x)的导函数,且y=3f′(x)的图象如图所示,则y=f(x)的单调递增开区间是(-∞,3).