题目内容
16.在△ABC中,角A,B,C的对边分别为a,b,c,满足b2-(a-c)2=(2-$\sqrt{3}$)ac(Ⅰ)求角B的大小;
(Ⅱ)若BC边上的中线AD的长为3,cos∠ADC=-$\frac{1}{4}$,求a的值.
分析 (Ⅰ)化简已知等式可得a2+c2-b2=$\sqrt{3}$ac,由余弦定理解得cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{\sqrt{3}}{2}$,结合B的范围,即可求B的值.
(Ⅱ)由同角三角函数基本关系式可求sin∠ADC,利用两角差的正弦函数公式可求sin∠BAD的值,由正弦定理,即可解得BD,从而可求a的值.
解答 (本题满分为12分)
解:(Ⅰ)在△ABC中,因为b2-(a-c)2=(2-$\sqrt{3}$)ac,
所以a2+c2-b2=$\sqrt{3}$ac,
由余弦定理得cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{\sqrt{3}ac}{2ac}$=$\frac{\sqrt{3}}{2}$,
又因为B为△ABC的内角,所以B=$\frac{π}{6}$.…(5分)
(Ⅱ)∵cos∠ADC=-$\frac{1}{4}$,
∴sin∠ADC=$\frac{\sqrt{15}}{4}$.
∴sin∠BAD=sin(∠ADC-$\frac{π}{6}$)=$\frac{3\sqrt{5}+1}{8}$.…(8分)
△ABD中,由正弦定理,得$\frac{AD}{sinB}=\frac{BD}{sin∠BAD}$,即$\frac{3}{\frac{1}{2}}=\frac{BD}{\frac{3\sqrt{5}+1}{8}}$,
解得BD=$\frac{9\sqrt{5}+3}{4}$,
故a=$\frac{9\sqrt{5}+3}{2}$.…(12分)
点评 本题主要考查了正弦定理,余弦定理,三角函数恒等变换在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.

| A. | [-2,-1] | B. | [-2,1] | C. | [-1,2] | D. | $[\frac{11}{4},4]$ |
| A. | {-1,0,1} | B. | {1} | C. | {-1,1} | D. | {0,1} |
 执行如图的程序框图,若输入k=63,则输出的n=( )
执行如图的程序框图,若输入k=63,则输出的n=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
| A. | 60° | B. | 30° | C. | 135° | D. | 120° |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形(称为事件A)的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形(称为事件B)的概率;
(3)根据以下用计算机所产生的20组随机数,试用随机数模拟的方法,来近似计算(2)中事件B的概率,
20组随机数如下:
| 组别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| X | 0.52 | 0.36 | 0.58 | 0.73 | 0.41 | 0.6 | 0.05 | 0.32 | 0.38 | 0.73 |
| Y | 0.76 | 0.39 | 0.37 | 0.01 | 0.04 | 0.28 | 0.03 | 0.15 | 0.14 | 0.86 |
| 组别 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| X | 0.67 | 0.47 | 0.58 | 0.21 | 0.54 | 0.64 | 0.36 | 0.35 | 0.95 | 0.14 |
| Y | 0.41 | 0.54 | 0.51 | 0.37 | 0.31 | 0.23 | 0.56 | 0.89 | 0.17 | 0.03 |
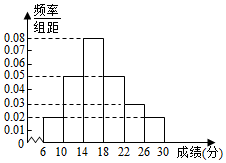 某省去年高三200000名考生英语听力考试服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如图方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30),如图是按上述分组方法得到的频率分布直方图.
某省去年高三200000名考生英语听力考试服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如图方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30),如图是按上述分组方法得到的频率分布直方图.