题目内容
在直角△ABC中，∠C=90°，∠A=30°，BC=1，D为斜边AB的中点，则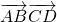 
=________．
-1
分析：根据含有30°角的直角三角形的性质，得到AB与CD的长度，求出两个向量的夹角是120°，利用向量的数量积公式写出表示式，得到结果．
解答：：∵∠C=90°，∠A=30°，BC=1，
∴AB=2．
∵D为斜边AB的中点，
∴CD=
AB=1，∠CDA=180°-30°-30°=120°．
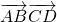∴=2×1×cos120°=-1，
故答案为：-1．
点评：本题考查平面向量的数量积的运算，考查含有30°角的直角三角形的性质，是一个基础题．
分析：根据含有30°角的直角三角形的性质，得到AB与CD的长度，求出两个向量的夹角是120°，利用向量的数量积公式写出表示式，得到结果．
解答：：∵∠C=90°，∠A=30°，BC=1，
∴AB=2．
∵D为斜边AB的中点，
∴CD=
AB=1，∠CDA=180°-30°-30°=120°．∴
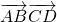=2×1×cos120°=-1，故答案为：-1．
点评：本题考查平面向量的数量积的运算，考查含有30°角的直角三角形的性质，是一个基础题．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
在直角△ABC中，CD是斜边AB上的高，则下列等式不成立的是（ ）
A、|
| ||||||||||||||
B、|
| ||||||||||||||
C、|
| ||||||||||||||
D、|
|
如图，在直角△ABC中，AB=AC=2，分别以A，B，C为圆心，以