题目内容
一组数据中的每一个数据都减去80,得一组新数据,若求得新数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是( )
| A、81.2,4.4 |
| B、78.8,4.4 |
| C、81.2,84.4 |
| D、78.8,75.6 |
考点:极差、方差与标准差
专题:概率与统计
分析:根据平均数和方差的定义,进行推导,即可得出答案.
解答:
解:设这组数据为x1,x2,…,xn,平均数为
,方差为s2;
则新数据为x1-80,x2-80,…,xn-80,
它的平均数是
=
=
=
-80
=1.2,
∴
=81.2;
方差为s′2=
[(x1-80-1.2)2+(x2-80-1.2)2+…+(xn-80-1.2)2]
=
[(x1-81.2)2+(x2-81.2)2+…+(xn-81.2)2]
=4.4=s2.
故选:A.
. |
| x |
则新数据为x1-80,x2-80,…,xn-80,
它的平均数是
. |
| x′ |
| (x1-80)+(x2-80)+…+(xn-80) |
| n |
=
| (x1+x2+…+xn)-80n |
| n |
=
. |
| x |
=1.2,
∴
. |
| x |
方差为s′2=
| 1 |
| n |
=
| 1 |
| n |
=4.4=s2.
故选:A.
点评:本题考查了平均数与方差的应用问题,解题时可以推导出正确的答案,是基础题目.

练习册系列答案
相关题目
执行如图中的程序框图,若p=0.8,则输出的n=( )
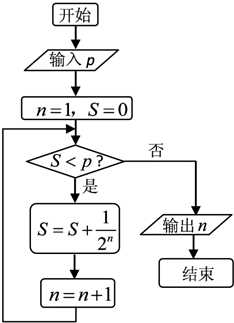

| A、2 | B、3 | C、5 | D、4 |
已知x,y满足
,则
的最大值为( )
|
| 2y+x |
| x |
| A、5 | B、3 | C、2 | D、6 |
 一个几何体的三视图如图所示,其中主视图、俯视图与左视图均是半径为2的圆,则这个几何体的表面积是
一个几何体的三视图如图所示,其中主视图、俯视图与左视图均是半径为2的圆,则这个几何体的表面积是


