题目内容
已知函数f(x)=x2-(a+2)x+alnx.其中常数a>0
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)设定义在D上的函数y=h(x)在点P(x0,h(x0))处的切线l的方程为y=g(x),当x≠x0时,若
>0在D内恒成立,则称P为y=h(x)的“类对称点”,当a=4时,试问y=f(x)是否存在“类对称点”?若存在,请至少求出一个“类对称点”的横坐标,若不存在,请说明理由.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)设定义在D上的函数y=h(x)在点P(x0,h(x0))处的切线l的方程为y=g(x),当x≠x0时,若
| h(x)-g(x) |
| x-x0 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)f(x)的定义域是(0,+∞),求出函数的导数,对a分情况进行讨论,
(Ⅱ)当a=4时,f(x)=x2-6x+4lnx,求出f′(x)=2x+
-6,得到令φ(x)=f(x)-g(x)=x2-6x+4lnx-(2x0+
-6)(x-x0)+x02-6x0+4lnx0,
求出函数φ(x)的导数,再通过讨论x的范围得出结论.
(Ⅱ)当a=4时,f(x)=x2-6x+4lnx,求出f′(x)=2x+
| 4 |
| x |
| 4 |
| x0 |
求出函数φ(x)的导数,再通过讨论x的范围得出结论.
解答:
解;(Ⅰ)f(x)的定义域是(0,+∞),
∴f′x)=2x-(a+2)+
=
=
,
①当
=1,即a=2时,f′(x)=
≥0,
∴f(x)的单调递增区间为(0,+∞),
②当
>1,即a>2时,
由f′(x)>0得:0<x<1或x>
,
由f(x)<0得:1<x<
;
∴f(x)的单调递增区间为(0,1)和(
,+∞),单调递减区间为(1,
)
③当
<1,即0<a<2时,
由f′(x)>0得:0<x<
或x>1,由f′(x)<0得:
<x<1
∴f(x)的单调递增区间为(0,
)和(1,+∞),单调递减区间为(
,1).
(Ⅱ)当a=4时,f(x)=x2-6x+4lnx,
∴f′(x)=2x+
-6,
y=g(x)=(2x0+
-6)(x-x0)+x02-6x0+4lnx0,
令φ(x)=f(x)-g(x)=x2-6x+4lnx-(2x0+
-6)(x-x0)+x02-6x0+4lnx0,
则φ(x0)=0,
φ′(x)=2x+
-6-(2x0+
-6)
=2(x-x0)(1-
)
=
(x-x0)(x0-
)
=
(x-x0)(
),
当x0<
时,φ(x)在(x0,
)上单调递减.
∴当x∈(x0,
)时,φ(x)<φ(x0)=0,
从而有x∈(x0,
)时,
<0,
当x0>
时,φ(x)在(
,x0)上单调递减.
∴当x∈(
,x0)时,φ(x)>φ(x0)=0,
从而有x∈(
,x0)时,
<0,
∴当x∈(0,
)∪(
,+∞)时,y=f(x)不存在“类对称点”.
当x0=
时,φ′(x)=
(x-
)2
∴φ(x)在(0,+∞)上是增函数,
故
>0,
所以当x0=
时,y=f(x)存在“类对称点”.
∴f′x)=2x-(a+2)+
| a |
| x |
=
| 2x2-(a+2)x+a |
| x |
=
| (2x-a)(x-1) |
| x |
①当
| a |
| 2 |
| 2(x-1)2 |
| x |
∴f(x)的单调递增区间为(0,+∞),
②当
| a |
| 2 |
由f′(x)>0得:0<x<1或x>
| a |
| 2 |
由f(x)<0得:1<x<
| a |
| 2 |
∴f(x)的单调递增区间为(0,1)和(
| a |
| 2 |
| a |
| 2 |
③当
| a |
| 2 |
由f′(x)>0得:0<x<
| a |
| 2 |
| a |
| 2 |
∴f(x)的单调递增区间为(0,
| a |
| 2 |
| a |
| 2 |
(Ⅱ)当a=4时,f(x)=x2-6x+4lnx,
∴f′(x)=2x+
| 4 |
| x |
y=g(x)=(2x0+
| 4 |
| x0 |
令φ(x)=f(x)-g(x)=x2-6x+4lnx-(2x0+
| 4 |
| x0 |
则φ(x0)=0,
φ′(x)=2x+
| 4 |
| x |
| 4 |
| x0 |
=2(x-x0)(1-
| 2 |
| x0x |
=
| 2 |
| x0 |
| 2 |
| x |
=
| 2 |
| x0 |
| x0x-2 |
| x |
当x0<
| 2 |
| 2 |
| x0 |
∴当x∈(x0,
| 2 |
| x0 |
从而有x∈(x0,
| 2 |
| x0 |
| φ(x) |
| x-x0 |
当x0>
| 2 |
| 2 |
| x0 |
∴当x∈(
| 2 |
| x0 |
从而有x∈(
| 2 |
| x0 |
| φ(x) |
| x-x0 |
∴当x∈(0,
| 2 |
| 2 |
当x0=
| 2 |
| 2 |
| x |
| 2 |
∴φ(x)在(0,+∞)上是增函数,
故
| φ(x) |
| x-x0 |
所以当x0=
| 2 |
点评:本题考察了函数的单调性,导数的应用,新概念的引出,渗透了分类讨论思想,本题是一道综合题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
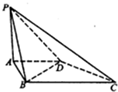 如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,AB⊥BC,平面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.
如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,AB⊥BC,平面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.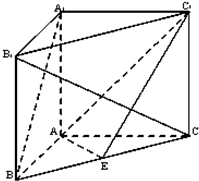 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1,且E是BC中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1,且E是BC中点. 设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B={x|-2<x<8}.
设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B={x|-2<x<8}.