题目内容
已知f(n)=1+
+
+…+
(n∈N*),计算得f(2)=
,f(4)>2,f(8)>
,f(16)>3,f(32)>
,由此推算:当n≥2时,有( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
A、f(2n)>
| ||
B、f(2n)>
| ||
C、f(2n)>
| ||
D、f(2n)>
|
考点:归纳推理
专题:推理和证明
分析:根据已知中的等式f(2)=
,f(4)>2,f(8)>
,f(16)>3,f(32)>
,…,我们分析等式左边数的变化规律及等式两边数的关系,归纳推断后,即可得到答案.
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
解答:
解:观察已知的等式:f(2)=
,
f(4)>2,即f(22)>
f(8)>
,即f(23)>
,
f(16)>3,即f(24)>
,
…,
归纳可得:
f(2n)>
,n∈N*)
故选:D.
| 3 |
| 2 |
f(4)>2,即f(22)>
| 2+2 |
| 2 |
f(8)>
| 5 |
| 2 |
| 2+3 |
| 2 |
f(16)>3,即f(24)>
| 2+4 |
| 2 |
…,
归纳可得:
f(2n)>
| n+2 |
| 2 |
故选:D.
点评:本题主要考查了归纳推理的问题,其一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
已知向量
=(1,x),
=(1,-x),若2
+
与
垂直,则|
|=( )
| a |
| b |
| a |
| b |
| b |
| a |
| A、4 | ||
| B、2 | ||
C、
| ||
D、
|
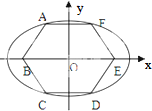 如图正六边形ABCDEF中,B、E为椭圆的焦点,A、C、D、F在椭圆上,则椭圆的离心率为( )
如图正六边形ABCDEF中,B、E为椭圆的焦点,A、C、D、F在椭圆上,则椭圆的离心率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知向量
=(λ,2),
=(1,-2),
⊥
,则实数λ=( )
| a |
| b |
| a |
| b |
| A、1 | B、4 | C、-1 | D、-4 |
已知实数x>y,且y≠0,则下列结论正确的是( )
A、
| ||||
| B、cx>cy(c∈R) | ||||
| C、x3>y3 | ||||
D、
|
掷一枚质地均匀的骰子,则掷得点数为1的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|



