题目内容
9.已知函数f(x)=2|x+1|-|x-1|(Ⅰ)求函数f的图象与直线y=1围成的封闭图形的面积m
(Ⅱ)在(Ⅰ)的条件下,若正数a、b满足a+2b=abm,求a+2b的最小值.
分析 (1)首先将函数的解析式写成分段函数的形式,然后绘制函数的图象,结合特殊的坐标即可求得面积值;
(2)利用(1)的结果结合均值不等式的结论求解最值即可.
解答 解:(1)函数$f(x)=2|x+1|-|x-1|=\left\{\begin{array}{l}{-x-3,x≤-1}\\{3x+1,-1<x<1}\\{x+3,x≥1}\end{array}\right.$,它的图象如图所示: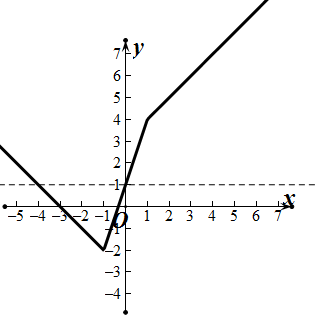
函数f(x)的图象与直线y=1的交点为(-2,1),(0,1),
故函数f(x)的图象和直线y=1围成的封闭图形的面积 $m=\frac{1}{2}×4×3=6$.
(2)由题意可得:a+2b=6ab,则 $\frac{1}{b}+\frac{2}{a}=6$,则:
$(a+2b)(\frac{1}{b}+\frac{2}{a})=\frac{a}{b}+\frac{4b}{a}+4≥2\sqrt{\frac{a}{b}×\frac{4b}{a}}+4=8$,
当且仅当$a=\frac{2}{3},b=\frac{1}{3}$ 时等号成立,
则x+2b的最小值是$\frac{8}{6}=\frac{4}{3}$.
点评 本题考查分段函数问题,函数图象的绘制,均值不等式的应用等,重点考查学生对基础概念的理解和计算能力,属于中等题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
17.2015年12月16日“第三届世界互联网大会”在中国乌镇举办,为了保护与会者的安全,将5个安保小组全部安排到指定三个区域内工作,且这三个区域每个区域至少有一个安保小组.则这样的安排的方法共有( )
| A. | 96种 | B. | 100种 | C. | 124种 | D. | 150种 |
4.已知角α(0°≤α<360)终边上一点的坐标为(sin235°,cos235°),则α=( )
| A. | 215° | B. | 225° | C. | 235° | D. | 245° |
14.已知|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,则$\overrightarrow a•\overrightarrow b$等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 2 | D. | 4 |
 如图,在梯形ABCD中,AB∥CD,$∠BCD=\frac{2π}{3}$,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF=1.
如图,在梯形ABCD中,AB∥CD,$∠BCD=\frac{2π}{3}$,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF=1.