题目内容
1.如图,在平面四边形ABCD中,若AC=6,($\overrightarrow{AB}+\overrightarrow{DC}$)•($\overrightarrow{AC}+\overrightarrow{BD}$)=11,则BD=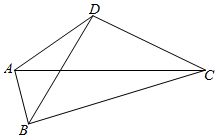
分析 取四边形各及对角线的中点,利用中位线定理把$\overrightarrow{AB}+\overrightarrow{DC}$,$\overrightarrow{AC}+\overrightarrow{BD}$用中位线所在向量表示出来,根据数量积列出方程解出BD.
解答 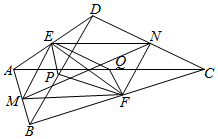 解分别取AD,BC,AB,CD,BD,AC的中点,E,F,M,N,P,Q.
解分别取AD,BC,AB,CD,BD,AC的中点,E,F,M,N,P,Q.
则四边形EPFQ,MFNE是平行四边形,
∴$\overrightarrow{AB}+\overrightarrow{DC}=2\overrightarrow{EP}+2\overrightarrow{EQ}=2\overrightarrow{EF}$=2($\overrightarrow{MF}-\overrightarrow{ME}$),$\overrightarrow{AC}+\overrightarrow{BD}=2\overrightarrow{MF}+2\overrightarrow{ME}$=2($\overrightarrow{MF}+\overrightarrow{ME}$),
∵($\overrightarrow{AB}+\overrightarrow{DC}$)•($\overrightarrow{AC}+\overrightarrow{BD}$)=11,
∴($\overrightarrow{MF}-\overrightarrow{ME}$)•($\overrightarrow{MF}+\overrightarrow{ME}$)=$\frac{11}{4}$,即${\overrightarrow{MF}}^{2}$-${\overrightarrow{ME}}^{2}$=$\frac{11}{4}$.
∴MF=$\frac{1}{2}AC=3$,ME=$\frac{1}{2}BD$,
∴9-$\frac{1}{4}B{D}^{2}$=$\frac{11}{4}$,
∴BD=5.
故答案为:5.
点评 本题考查了平面向量线性运算的几何意义,属于中档题.

| A. | 210 | B. | 120 | C. | 90 | D. | 80 |
| A. | -2-3i | B. | -2+3i | C. | 2-3i | D. | 2+3i |
| A. | 3 | B. | 6 | C. | -3 | D. | -6 |