题目内容
13.已知角θ的终边在直线y=-2x上,则tan(-$\frac{π}{4}$+θ)-5cos2θ=( )| A. | 3 | B. | 6 | C. | -3 | D. | -6 |
分析 利用已知条件求出正切函数值,然后化简求解即可.
解答 解:角θ的终边在直线y=-2x上,可得tanθ=-2.
则tan(-$\frac{π}{4}$+θ)-5cos2θ=$\frac{tanθ-tan\frac{π}{4}}{1+tanθtan\frac{π}{4}}$-$\frac{5co{s}^{2}θ-5si{n}^{2}θ}{co{s}^{2}θ+si{n}^{2}θ}$
=$\frac{-2-1}{1-2}$+$\frac{5-5tanθ}{1+ta{n}^{2}θ}$
=3+$\frac{5+10}{1+4}$
=6.
故选:B.
点评 本题考查三角函数的化简求值,考查转化思想以及计算能力.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
4.定义在[0,+∞)的函数f(x)的导函数为f′(x),对于任意的x≥0,恒有f′(x)>f(x),a=e3f(2),b=e2f(3),则a,b的大小关系是( )
| A. | a>b | B. | a<b | C. | a=b | D. | 无法确定 |
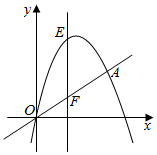 如图所示,已知二次函数y=-x2+4x+c的图象经过坐标原点,并且与函数y=x的图象交于O,A两点.求:
如图所示,已知二次函数y=-x2+4x+c的图象经过坐标原点,并且与函数y=x的图象交于O,A两点.求: