题目内容
9．在复平面内，复数z1对应的点与复数z2=$\frac{3+2i}{i}$（i为虚数单位）对应的点关于虚轴对称，则z1等于（ ）| A． | -2-3i | B． | -2+3i | C． | 2-3i | D． | 2+3i |
分析 利用复数代数形式的乘除运算化简，求得z2的坐标，进一步得到z1的坐标得答案．
解答 解：∵z2=$\frac{3+2i}{i}$=$\frac{（3+2i）（-i）}{-{i}^{2}}=2-3i$，
∴z2在复平面内对应点的坐标为（2，-3），
又复数z1对应的点与复数z2对应的点关于虚轴对称，
∴z1所对应点的坐标为（-2，-3），则z1=-2-3i．
故选：A．
点评 本题考查复数代数形式的乘除运算，考查了复数的代数形式的表示法及其几何意义，是基础的计算题．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
4．定义在[0，+∞）的函数f（x）的导函数为f′（x），对于任意的x≥0，恒有f′（x）＞f（x），a=e3f（2），b=e2f（3），则a，b的大小关系是（ ）
| A． | a＞b | B． | a＜b | C． | a=b | D． | 无法确定 |
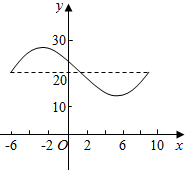函数y=Asin（ωx+θ）+b的图象如图所示，则此函数的解析式为y=y=10sin（$\frac{π}{8}$x+$\frac{3π}{4}$）+20．