题目内容


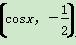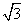已知向量a＝，b＝(sinx，cos2x)，x∈R，设函数f(x)＝a·b.

(1)求f(x)的最小正周期；

(2)求f(x)在上的最大值和最小值．

 


　f(x)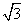＝·(sinx，cos2x)

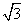＝cosxsinx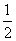－cos2x＝sin2x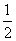－cos2x

＝cossin2x－sincos2x＝sin.

(1)f(x)的最小正周期为，

即函数f(x)的最小正周期为π.

(2)∵0≤x≤，∴－≤2x－≤.由正弦函数的性质，知当2x－＝，即x＝时，f(x)取得最大值1，

当2x－＝－，即x＝0时，f(x)取得最小值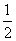－.因此，f(x)在[0，]上的最大值是1，最小值是－.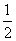


练习册系列答案
相关题目

已知函数f(x)＝ex－m－x，其中m为常数．

(1)若对任意x∈R有f(x)≥0恒成立，求m的取值范围；

(2)当m>1时，判断f(x)在[0,2m]上零点的个数，并说明理由．

已知α∈，sinα＝.

(1)求sin的值；

(2)求cos的值．

定义运算＝ad－bc，若cosα＝，＝，0<β<α<，则β等于(　　)

已知函数y＝2sin(ωx＋θ)为偶函数(ω>0,0<θ<π)，其图象与直线y＝2的交点的横坐标为x1，x2，若|x1－x2|的最小值为π，则(　　)

A．ω＝2，θ＝                        B．ω＝，θ＝

C．ω＝，θ＝                       D．ω＝2，θ＝

已知向量a＝(cosωx－sinωx，sinωx)，b＝(－cosωx－sinωx,2cosωx)，设函数f(x)＝a·b＋λ(x∈R)的图象关于直线x＝π对称，其中ω，λ为常数，且ω∈.

(1)求函数f(x)的最小正周期；

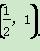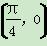(2)若y＝f(x)的图象经过点，求函数f(x)在区间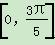上的取值范围．

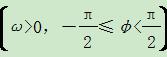将函数f(x)＝sin(ωx＋φ)图象上每一点的横坐标缩短为原来的一半，纵坐标不变，再向右平移个单位长度得到y＝sinx的图象，则f＝________.

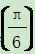在△ABC中，已知＝tanA，当A＝时，△ABC的面积为________．

已知点A(1,3)，B(4，－1)，则与向量同方向的单位向量为(　　)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网