题目内容
已知|x|+|x-1|≥2m-3对任意实数x恒成立,则实数m的最大值为 .
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:利用绝对值三角不等式求得|x|+|x-1|≥1,结合题意可得 1≥2m-3,从而求得m的最大值.
解答:
解:∵|x|+|x-1|≥|x-(x+1)|=1,|x|+|x-1|≥2m-3对任意实数x恒成立,
∴1≥2m-3,解得 m≤2,即m的最大值为2,
故答案为:2.
∴1≥2m-3,解得 m≤2,即m的最大值为2,
故答案为:2.
点评:本题主要考查绝对值三角不等式,函数的恒成立问题,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
若向量
=(3,m),
=(2,-1),
⊥
,则实数m的值为( )
| a |
| b |
| a |
| b |
A、-
| ||
B、
| ||
| C、2 | ||
| D、6 |
 已知正三棱柱(侧棱与底面垂直,底面是正三角形)的高与底面边长均为2,其直观图和正视图如下,则它的侧视图的面积是( )
已知正三棱柱(侧棱与底面垂直,底面是正三角形)的高与底面边长均为2,其直观图和正视图如下,则它的侧视图的面积是( )A、2
| ||
| B、4 | ||
C、
| ||
| D、12 |
阅读如图所示的程序框图,运行相应的程序,输出的结果是( )


| A、3 | B、13 | C、33 | D、123 |
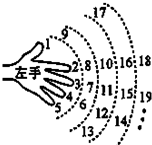 如图,一个小朋友按如图所示的规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,…,一直数到2014时,对应的指头是
如图,一个小朋友按如图所示的规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,…,一直数到2014时,对应的指头是