题目内容
(本小题满分12分)
设函数 其中
其中 .
.
(Ⅰ)证明: 是
是 上的减函数;
上的减函数;
(Ⅱ)若 ,求
,求 的取值范围.
的取值范围.
(1)利用函数单调性定义,设变量,作差,变形,定号,得到结论。
(2)
解析试题分析:(Ⅰ)设
则
 又
又
 在
在 上是减函数························· 6分
上是减函数························· 6分
(Ⅱ) ····················· 8分
····················· 8分 从而
从而  ········ 10分
········ 10分 的取值范围是
的取值范围是 ·························· 12分
·························· 12分
考点:本试题主要是考查了函数单调性以及不等式的求解。
点评:函数单调性的证明一般用定义法。先设变量,作差(或作商),变形,定号,下结论。
同时对于含有参数的对数不等式的求解,底数不定要分类讨论,属于中档题。

练习册系列答案
相关题目
 (万元)和
(万元)和 (万元),它们与投入资金
(万元),它们与投入资金 (万元)的关系有经验公式:
(万元)的关系有经验公式: 。今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?
。今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?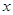 天(
天(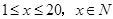 )的销售价格(单位:元)为
)的销售价格(单位:元)为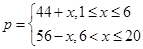 ,第
,第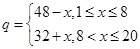 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元.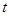 关于第
关于第 为常数,且
为常数,且 )满足条件:
)满足条件: ,且方程
,且方程 有两个相等的实数根.
有两个相等的实数根. 的解析式;
的解析式; 上的最大值和最小值;
上的最大值和最小值;
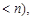 使
使 和
和 ,如果存在,求出
,如果存在,求出 的值,如不存在,请说明理由.
的值,如不存在,请说明理由.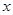 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为 万元,且
万元,且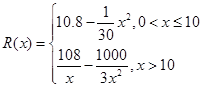 .
.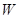 (万元)关于年产量
(万元)关于年产量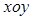 ,
, 轴在地平面上,
轴在地平面上,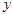 轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在
轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在 表示的曲线上,其中
表示的曲线上,其中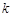 与发射方向有关,炮的射程是指炮弹落地点的横坐标.
与发射方向有关,炮的射程是指炮弹落地点的横坐标.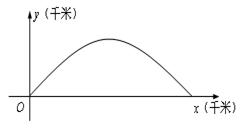
 不超过多少时,炮弹可以击中它?请说明理由.
不超过多少时,炮弹可以击中它?请说明理由.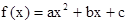 满足:
满足: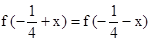 ,且
,且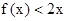 的
的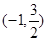
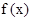 的解析式;
的解析式;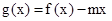
 ,若
,若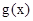 在
在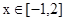 上的最小值为-4,求
上的最小值为-4,求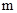 的值.
的值.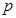 与每日生产产品件数
与每日生产产品件数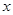 (
(
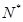 )间的关系为
)间的关系为 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.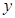 (元)表示成日产量
(元)表示成日产量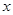 (单位:辆/千米)的函数。当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当2
(单位:辆/千米)的函数。当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当2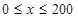 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.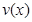 的表达式;
的表达式;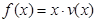 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).