题目内容
6．已知向量$\overrightarrow{a}$=（sinx-cosx，2cosx），$\overrightarrow{b}$=（sinx+cosx，sinx）（1）若$\overrightarrow{a}$⊥$\overrightarrow{b}$，求tan2x的值；
（2）若$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{3}{5}$，求sin4x的值．
分析 （1）由$\overrightarrow{a}$⊥$\overrightarrow{b}$得$\overrightarrow{a}•\overrightarrow{b}$=0，可列式求tan2x
（2）由$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{3}{5}$，得$\overrightarrow{a•}\overrightarrow{b}$=$\frac{3}{5}$，即 sin2x-cos2x=$\frac{3}{5}$，再平方即可．
解答 解：（1）∵$\overrightarrow{a}$⊥$\overrightarrow{b}$，∴$\overrightarrow{a}•\overrightarrow{b}=（sinx-cosx）（sinx+cosx）+2sinxcosx$=sin2x-cos2x=0
∴tan2x=1
（2）∵$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{3}{5}$，∴，∴$\overrightarrow{a}•\overrightarrow{b}=（sinx-cosx）（sinx+cosx）+2sinxcosx$=sin2x-cos2x=$\frac{3}{5}$，
（ sin2x-cos2x）2=1-sin4x=$\frac{9}{25}$，∴sin4x=$\frac{16}{25}$．
点评 本题考查了向量的数量积运算，属于基础题．
练习册系列答案
相关题目
16．
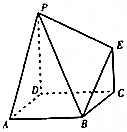如图，多面体ABCDPE的底面ABCD是平行四边形，AD=AB=2，$\overrightarrow{AB}$•$\overrightarrow{AD}$=0，PD⊥平面ABCD，EC∥PD，且PD=2EC=2，则二面角A-PB-E的大小为（ ）
如图，多面体ABCDPE的底面ABCD是平行四边形，AD=AB=2，$\overrightarrow{AB}$•$\overrightarrow{AD}$=0，PD⊥平面ABCD，EC∥PD，且PD=2EC=2，则二面角A-PB-E的大小为（ ）| A． | $\frac{2π}{3}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{3}$ | D． | $\frac{5π}{6}$ |
11．已知函数f（x）=x2+tx+t，?x∈R，f（x）＞0，函数g（x）=3x2-2（t+1）x+t，则“?a，b∈（0，1）使得g（a）=g（b）=0”为真命题的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
18．抛物线y2=2x的准线方程为（ ）
| A． | x=1 | B． | x=$\frac{1}{2}$ | C． | x=-1 | D． | x=-$\frac{1}{2}$ |
15．M是抛物线C：y2=2px（p＞0）上一点，F是抛物线C的焦点，O为坐标原点，若|MF|=p，K是抛物线C准线与x轴的交点，则∠MKO=（ ）
| A． | 15° | B． | 30° | C． | 45° | D． | 60° |
16．过点P在双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的右支上，其左、右焦点分别为F1，F2，PF1的垂直平分线过F2，且原点到直线PF1的距离恰好等于双曲线的实半轴长，则该双曲线的离心率为（ ）
| A． | $\frac{7}{3}$ | B． | $\frac{5}{3}$ | C． | $\frac{5}{4}$ | D． | $\frac{7}{4}$ |