题目内容
5.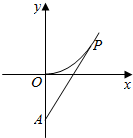 中国海警缉私船对一艘走私船进行定位:以走私船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度).中国海警缉私船恰在走私船正南方18海里A处(如图).现假设:①走私船的移动路径可视为抛物线y=$\frac{9}{28}$x2;②定位后中国海警缉私船即刻沿直线匀速前往追埔;③中国海警缉私船出发t小时后,走私船所在的位置的横坐标为2$\sqrt{7}$t.
中国海警缉私船对一艘走私船进行定位:以走私船的当前位置为原点,以正北方向为y轴正方向建立平面直角坐标系(以1海里为单位长度).中国海警缉私船恰在走私船正南方18海里A处(如图).现假设:①走私船的移动路径可视为抛物线y=$\frac{9}{28}$x2;②定位后中国海警缉私船即刻沿直线匀速前往追埔;③中国海警缉私船出发t小时后,走私船所在的位置的横坐标为2$\sqrt{7}$t.(1)当t=1,写出走私船所在位置P的纵坐标,若此时两船恰好相遇,求中国海警缉私船速度的大小;
(2)问中国海警缉私船的时速至少是多少海里才能追上走私船?
分析 (1)t=1时,确定P的横坐标,代入抛物线方程可得P的纵坐标,利用|AP|,即可确定中国海警缉私船速度的大小;
(2)设中国海警缉私船的时速为v海里,经过t小时追上走私船,此时位置为(2$\sqrt{7}$t,9t2),从而可得v关于t的关系式,利用基本不等式,即可得到结论.
解答 解:(1)t=1时,P的横坐标xP=2$\sqrt{7}$,代入抛物线方程y=$\frac{9}{28}$x2中,得P的纵坐标yP=9.
由A(0,-18),可得|AP|=$\sqrt{757}$,得中国海警缉私船速度的大小为$\sqrt{757}$海里/时;
(2)设中国海警缉私船的时速为v海里,经过t小时追上走私船,此时位置为(2$\sqrt{7}$t,9t2).
由vt=|AP|=$\sqrt{81({t}^{4}+4)+352{t}^{2}}$,整理得v2=81(t2+$\frac{4}{{t}^{2}}$)+352
因为t2+$\frac{4}{{t}^{2}}$≥4,当且仅当t=$\sqrt{2}$时等号成立,所以v2≥81×4+352=262,即v≥26.
因此,中国海警缉私船的时速至少是26海里才能追上走私船.
点评 本题主要考查函数模型的选择与运用.选择恰当的函数模型是解决此类问题的关键,属于中档题.

练习册系列答案
相关题目
16.在下列各图中,两个变量具有较强正相关关系的散点图是( )
| A. |  | B. |  | C. |  | D. |  |
13.点M,N分别是正方体ABCD-A1B1C1D1的棱BB1和B1C1的中点,则异面直线CM与DN所成的角的余弦值为( )
| A. | $\frac{{4\sqrt{5}}}{15}$ | B. | $\frac{{\sqrt{5}}}{15}$ | C. | $\frac{{\sqrt{3}}}{15}$ | D. | $\frac{4}{15}$ |
20.我国古代数学巨著《九章算术》中,有如下问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”这个问题用今天的白话叙述为:有一位善于织布的女子,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这位女子每天分别织布多少?”根据上题的已知条件,可求得该女子第4天所织布的尺数为”( )
| A. | $\frac{8}{15}$ | B. | $\frac{16}{15}$ | C. | $\frac{20}{31}$ | D. | $\frac{40}{31}$ |