题目内容
设0≤α≤π,不等式8x2-(8sin α)x+cos 2α≥0对x∈R恒成立,则α的取值范围为 .
[0,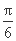 ]∪[
]∪[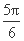 ,π]
,π]

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
题目内容
设0≤α≤π,不等式8x2-(8sin α)x+cos 2α≥0对x∈R恒成立,则α的取值范围为 .
[0,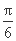 ]∪[
]∪[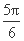 ,π]
,π]

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案