题目内容
双曲线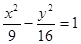 上的点M到点(-5,0)的距离为7,则M到点(5,0)的距离为( )
上的点M到点(-5,0)的距离为7,则M到点(5,0)的距离为( )
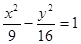 上的点M到点(-5,0)的距离为7,则M到点(5,0)的距离为( )
上的点M到点(-5,0)的距离为7,则M到点(5,0)的距离为( )| A.1或13 | B.15 | C.13 | D.1 |
C
试题分析:易知双曲线的焦点坐标为(
 5,0),因为点M到点(-5,0)的距离为7<a+c=8,所以点M一定在双曲线的左之上,设所求距离为d,所以由双曲线的定义知d-7=6,所以d=13.
5,0),因为点M到点(-5,0)的距离为7<a+c=8,所以点M一定在双曲线的左之上,设所求距离为d,所以由双曲线的定义知d-7=6,所以d=13.点评:此题易错选A,其主要原因是没判断出点M在双曲线的哪一支上。

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
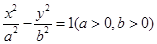 过其左焦点F1作x轴的垂线交双曲线于A,B两点,若双曲线右顶点在以AB为直径的圆内,则双曲线离心率的取值范围为
过其左焦点F1作x轴的垂线交双曲线于A,B两点,若双曲线右顶点在以AB为直径的圆内,则双曲线离心率的取值范围为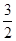 ,+∞)
,+∞) 的渐近线方程为
的渐近线方程为  上一点
上一点 到左焦点的距离为4,则点
到左焦点的距离为4,则点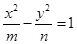 的离心率为
的离心率为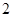 ,且双曲线的一个焦点恰好是抛物线
,且双曲线的一个焦点恰好是抛物线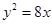 的
的 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则 等于
等于


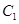 :
: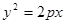 的准线经过双曲线
的准线经过双曲线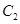 :
: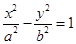 的左焦点,若抛物线
的左焦点,若抛物线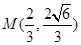 .
.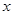 轴上的双曲线
轴上的双曲线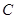 的两条渐近线过坐标原点,且两条渐近线
的两条渐近线过坐标原点,且两条渐近线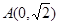 为圆心,1为半径的圆相切,又知
为圆心,1为半径的圆相切,又知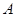 关于直线
关于直线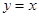
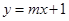 与双曲线
与双曲线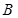 两点,另一直线
两点,另一直线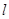 经过
经过 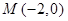 及
及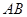 的中点,求直线
的中点,求直线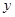 轴上的截距
轴上的截距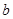 的取值范围.
的取值范围.  的右焦点
的右焦点 与圆
与圆 (极坐标方程)的圆心重合,点
(极坐标方程)的圆心重合,点 ,则双曲线的离心率为( )
,则双曲线的离心率为( )


