题目内容
【题目】已知数列{an}的前n项和为Sn , 且满足12Sn﹣36=3n2+8n,数列{log3bn}为等差数列,且b1=3,b3=27.
(Ⅰ)求数列{an}与{bn}的通项公式;
(Ⅱ)令cn=(﹣1)n ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
【答案】解:(1)由题意得 ![]() ,∴a1=
,∴a1= ![]() =
= ![]() ,
,
当n≥2时,an=Sn﹣Sn﹣1= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣3=
﹣3= ![]() +
+ ![]() ,
,
又 ![]() =
= ![]() ≠
≠ ![]() ,
,
∴an=  .
.
设等差数列{log3bn}的公差为d,且b1=3,b3=27.
∴2d=log327﹣log33=3﹣1,解得d=1.
∴log3bn=log33+(n﹣1)=n,
∴bn=3n.
(Ⅱ)由(Ⅰ)得, 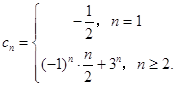
当n=1, ![]() .
.
当n≥2时,Tn= ![]()
= ![]() ,
,
当n为奇数时, ![]()
= 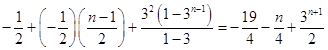 ,n=1适合此式;
,n=1适合此式;
当n为偶数时, ![]()
= ![]() ,
,
综上,Tn= 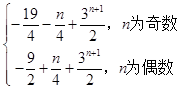
【解析】(1)由题意得 ![]() ,可得a1=
,可得a1= ![]() ,当n≥2时,an=Sn﹣Sn﹣1.可得an.设等差数列{log3bn}的公差为d,且b1=3,b3=27.可得2d=log327﹣log33.可得bn.(Ⅱ)由(Ⅰ)得,
,当n≥2时,an=Sn﹣Sn﹣1.可得an.设等差数列{log3bn}的公差为d,且b1=3,b3=27.可得2d=log327﹣log33.可得bn.(Ⅱ)由(Ⅰ)得, 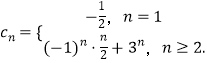 当n=1,
当n=1, ![]() .当n≥2时,Tn=
.当n≥2时,Tn= ![]()
= ![]() ,对n分类讨论即可得出.
,对n分类讨论即可得出.
【考点精析】关于本题考查的数列的前n项和和等差数列的性质,需要了解数列{an}的前n项和sn与通项an的关系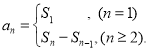 ;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列才能得出正确答案.
;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列才能得出正确答案.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】某校举行高二理科学生的数学与物理竞赛,并从中抽取72名学生进行成绩分析,所得学生的及格情况统计如表:
物理及格 | 物理不及格 | 合计 | |
数学及格 | 28 | 8 | 36 |
数学不及格 | 16 | 20 | 36 |
合计 | 44 | 28 | 72 |
(1)根据表中数据,判断是否是99%的把握认为“数学及格与物理及格有关”;
(2)若以抽取样本的频率为概率,现在该校高二理科学生中,从数学及格的学生中随机抽取3人,记X为这3人中物理不及格的人数,从数学不及格学生中随机抽取2人,记Y为这2人中物理不及格的人数,记ξ=|X﹣Y|,求ξ的分布列及数学期望. 附:x2= ![]() .
.
P(X2≥k) | 0.150 | 0.100 | 0.050 | 0.010 |
k | 2.072 | 2.706 | 3.841 | 6.635 |