题目内容
【题目】已知椭圆E： 
的左、右焦点分别为F1 ， F2 ， 左、右顶点分别为A，B．以F1F2为直径的圆O过椭圆E的上顶点D，直线DB与圆O相交得到的弦长为 
．设点P（a，t）（t≠0），连接PA交椭圆于点C，坐标原点为O．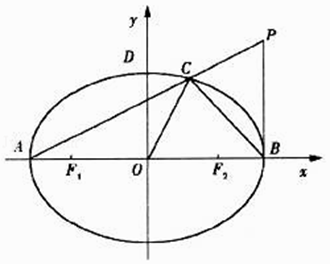
（I）求椭圆E的方程；
（II）若三角形ABC的面积不大于四边形OBPC的面积，求|t|的最小值．
【答案】解：（Ⅰ）因为以F1，F2为直径的圆O过点D，所以b=c，则圆O的方程为x2+y2=b2，
又a2=b2+c2，所以 
，直线DB的方程为 
，直线DB与圆O相交得到的弦长为 
，
则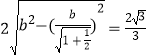 
，所以b=1， 
，
所以椭圆E的方程为 
．
（Ⅱ）由已知得： ，b=1，椭圆方程为 ，
设直线PA的方程为 
，由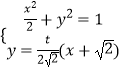 
整理得 
，
解得： 
， 
，则点C的坐标是 
，
故直线BC的斜率为 
，由于直线OP的斜率为 
，
所以kBCkOP=﹣1，所以OP⊥BC．
所以 
， 
，所以 
，
整理得2+t2≥4， 
，所以 
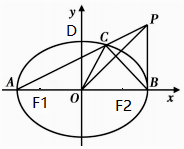
【解析】（Ⅰ）由题意可知：b=c，则 ，则直线DB的方程为 ，由题意可知 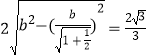，即可求得b及a的值，求得椭圆方程；（2）设直线PA的方程为 ，代入椭圆方程，求得C点坐标，直线BC的斜率为 ，由于直线OP的斜率为 ，可得OP⊥BC，分别求得三角形ABC的面积及四边形OBPC的面积由 ，即可求得丨t丨取值范围，即可求得|t|的最小值．
练习册系列答案
相关题目
