题目内容
已知, 点O是正方体ABCD-A1B1C1D1上底面A
BCD的中心，M是正方体对角线AC1和截面A1BD的交点.
求证：O、M、A1三点共线.
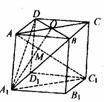
证明: 如图, 连结AC、A1C1，A1、O都是平面A1BD和平面AA1C1C的公共点，
由AC
平面A1BD=M，AC
平面AA1C1C，得M是平面A1BD和平面AA1C1C的公共点，于是O、M、A1都是这两个平面的公共点，故在其交线上，得三点共线.
练习册系列答案
相关题目
题目内容
已知, 点O是正方体ABCD-A1B1C1D1上底面ABCD的中心，M是正方体对角线AC1和截面A1BD的交点.
求证：O、M、A1三点共线.
证明: 如图, 连结AC、A1C1，A1、O都是平面A1BD和平面AA1C1C的公共点，
由AC平面A1BD=M，AC平面AA1C1C，得M是平面A1BD和平面AA1C1C的公共点，于是O、M、A1都是这两个平面的公共点，故在其交线上，得三点共线.
已知正方体ABCD-A′B′C′D′的棱长为1，点M是棱AA′的中点，点O是对角线BD′的中点．
已知正方体ABCD-A'B'C'D'的棱长为1，点M是棱AA'的中点，点O是对角线BD'的中点．
已知点O为正方体ABCD-A1B1C1D1底面ABCD的中心，则下列结论正确的是（ ）
已知正方体ABCD-A'B'C'D'的棱长为1，点M是棱AA'的中点，点O是对角线BD'的中点．