题目内容
已知点O为正方体ABCD-A1B1C1D1底面ABCD的中心，则下列结论正确的是（ ）分析：取上底面的中心为E，连接A1E、CE、OC，欲证直线OA1∥平面CB1D1，根据直线与平面平行的判定定理可知只需证OA1与平面CB1D1内一直线平行，而A1O∥EC，A1O?平面CB1D1，EC?平面CB1D1满足定理所需条件，即可可得到结论．
解答：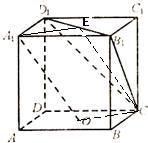
解：根据正方体的性质可知A1E=OC，A1E∥OC
∴四边形A1ECO为平行四边形
则A1O∥EC
而A1O?平面CB1D1，EC?平面CB1D1
∴直线OA1∥平面CB1D1
故选D
解：根据正方体的性质可知A1E=OC，A1E∥OC∴四边形A1ECO为平行四边形
则A1O∥EC
而A1O?平面CB1D1，EC?平面CB1D1
∴直线OA1∥平面CB1D1
故选D
点评：此题考查了正方体的特征，同时考查了线面位置关系、线线位置关系的判定，属于基础题．
练习册系列答案
相关题目
（甲）如图，已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC，∠ABC=90°，BC=2，AC=
的正方体ABCD-A1B1C1D1，它的外接球的球心为O，点E是AB的中点，点P是球O的球面上任意一点，有以下判断：①该正方体外接球的体积是36π；②异面直线OE与B1C所成角为90°；③PE长的最大值为
；④过点E的平面截球O的截面面积的最小值为6π．其中所有正确判断的序号是 ．
，又AA1⊥A1C，AA1=A1C．