题目内容
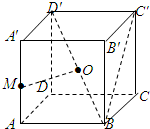 已知正方体ABCD-A'B'C'D'的棱长为1,点M是棱AA'的中点,点O是对角线BD'的中点.
已知正方体ABCD-A'B'C'D'的棱长为1,点M是棱AA'的中点,点O是对角线BD'的中点.(Ⅰ)求证:OM为异面直线AA'和BD'的公垂线;
(Ⅱ)求三棱锥M-OBC的体积;
(Ⅲ)求二面角M-BC'-B'的正切值.
分析:(Ⅰ)连接AC,取AC中点K,则K为BD的中点,连接OK因为M是棱AA′的中点,点O是BD′的中点,证明MO⊥AA′,MO⊥BD′,证明OM为异面直线AA'和BD'的公垂线.
(Ⅱ)求出点O到平面MA′D′距离h,利用VM-OBC=VM-OA′D′=VO-MA′D′=
S△MA′D′h,求出体积.
(Ⅲ)取′BB′中点N,连接MN,则MN⊥平面BCC′B′,过点N作NH⊥BC′于H,连接MH,
说明∠MHN为二面角M-BC′-B′的平面角,在Rt△MNH中,求出tan∠MHN即可.
(Ⅱ)求出点O到平面MA′D′距离h,利用VM-OBC=VM-OA′D′=VO-MA′D′=
| 1 |
| 3 |
(Ⅲ)取′BB′中点N,连接MN,则MN⊥平面BCC′B′,过点N作NH⊥BC′于H,连接MH,
说明∠MHN为二面角M-BC′-B′的平面角,在Rt△MNH中,求出tan∠MHN即可.
解答: 解:(Ⅰ)证明:连接AC,取AC中点K,则K为BD的中点,连接OK因为M是棱AA′的中点,点O是BD′的中点,所以AM
解:(Ⅰ)证明:连接AC,取AC中点K,则K为BD的中点,连接OK因为M是棱AA′的中点,点O是BD′的中点,所以AM
DD′
OK
所以MO
AK…(1分)
由AA′⊥AK,得MO⊥AA′…(2分)
因为AK⊥BD,AK⊥BB′,所以AK⊥平面BDD′B′
所以AK⊥BD′
所以MO⊥BD′…(3分)
又因为OM是异面直线AA′和BD′都相交
故OM为异面直线AA'和BD'的公垂线…(4分)
(Ⅱ)易知,S△OBC=S△OA′D′,…(10分)
且△OBC和△OA′D′都在平面BCD′A′内,点O到平面MA′D′距离h=
…(11分)
VM-OBC=VM-OA′D′=VO-MA′D′=
S△MA′D′h=
…(14分)
(Ⅲ)取′BB′中点N,连接MN,则MN⊥平面BCC′B′,过点N作NH⊥BC′于H,连接MH,则由三垂线定理得BC′⊥MH
从而,∠MHN为二面角M-BC′-B′的平面角…(6分)
MN=1,NH=Bnsin45°=
×
=
…(7分)
在Rt△MNH中,tan∠MHN=
=
=2
故二面角M-BC′-B′的正切值的大小为2
…(9分)
 解:(Ⅰ)证明:连接AC,取AC中点K,则K为BD的中点,连接OK因为M是棱AA′的中点,点O是BD′的中点,所以AM
解:(Ⅰ)证明:连接AC,取AC中点K,则K为BD的中点,连接OK因为M是棱AA′的中点,点O是BD′的中点,所以AM| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
所以MO
| ∥ |
. |
由AA′⊥AK,得MO⊥AA′…(2分)
因为AK⊥BD,AK⊥BB′,所以AK⊥平面BDD′B′
所以AK⊥BD′
所以MO⊥BD′…(3分)
又因为OM是异面直线AA′和BD′都相交
故OM为异面直线AA'和BD'的公垂线…(4分)
(Ⅱ)易知,S△OBC=S△OA′D′,…(10分)
且△OBC和△OA′D′都在平面BCD′A′内,点O到平面MA′D′距离h=
| 1 |
| 2 |
VM-OBC=VM-OA′D′=VO-MA′D′=
| 1 |
| 3 |
| 1 |
| 24 |
(Ⅲ)取′BB′中点N,连接MN,则MN⊥平面BCC′B′,过点N作NH⊥BC′于H,连接MH,则由三垂线定理得BC′⊥MH
从而,∠MHN为二面角M-BC′-B′的平面角…(6分)
MN=1,NH=Bnsin45°=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
在Rt△MNH中,tan∠MHN=
| MN |
| NH |
| 1 | ||||
|
| 2 |
故二面角M-BC′-B′的正切值的大小为2
| 2 |
点评:本小题主要考查异面直线、直线与平面垂直、二面角、正方体、三棱锥体积等基础知识,并考查空间想象能力和逻辑推理能力,考查应用向量知识解决数学问题的能力.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1= 已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.