题目内容
17．定义在R上的函数f（x）对任意两个不相等实数a、b，且a＜b总有f（a）＜f（b）成立，则必有（ ）| A． | f（x）先增加后减少 | B． | f（x）先减少后增加 | C． | f（x）在R上是增函数 | D． | f（x）在R上是减函数 |
分析 根据函数单调性的定义判断即可．
解答 解：定义在R上的函数f（x）对任意两个不相等实数a、b，
对于a＜b，总有f（a）＜f（b）成立，
根据函数单调性的定义得：f（x）在R递增，
故选：C．
点评 本题考查了函数的单调性的定义，是一道基础题．
练习册系列答案
相关题目
8．已知函数f（x）是定义在R上的偶函数，且对任意x∈R，都有f（x-1）=f（x+3）．当x∈[4，5]时，f（x）=2x+1，设函数f（x）在区间[-2，0]上的反函数为f-1（x），则f-1（19）的值为（ ）
| A． | -log23 | B． | -2log23 | C． | 1-log23 | D． | 3-2log23 |
12．若关于x的不等式x2+ax-2＞0在区间[1，2]上有解，则实数a的取值范围为（ ）
| A． | （-∞，-1） | B． | （-∞，1） | C． | （1，+∞） | D． | （-1，+∞） |
2．下列函数是偶函数的是（ ）
| A． | y=x3 | B． | y=3x | C． | y=2x2-1 | D． | y=x2+2x-1 |
9．已知等差数列{an}中，a2+a4=16，a1=1，则a5的值是（ ）
| A． | 15 | B． | 30 | C． | 31 | D． | 64 |
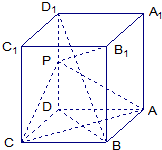如图，长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，点P为DD1的中点．求：
