Question

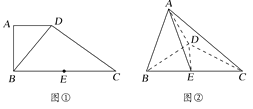
【题目】如图①，在直角梯形ABCD中，AD＝1，AD∥BC，AB⊥BC，BD⊥DC，点E是BC边的中点，将△ABD沿BD折起，使平面ABD⊥平面BCD，连接AE，AC，DE，得到如图②所示的几何体.

(1)求证：AB⊥平面ADC；

(2)若AC与平面ABD所成角的正切值为，求二面角B—AD—E的余弦值。

Answer 1

【答案】（1）详见解析；（2）.

【解析】

（1）要证明线面垂直，由条件可知，再根据面面垂直转化为证明，再根据线面垂直判断定理证明；

（2）由（1）可知，因为AD＝1，所以CD＝，设AB＝x(x>0)，则BD＝，因为△ABD∽△DCB，所以＝，即，求得边长，再取过A作AOBD于O，则AO平面BDC，过O作OG//DC交BC于G，以O为坐标原点 OB，OG，OA分别为x.y.z轴非负半轴建立空间直角坐标系，利用向量的坐标法求二面角的余弦值.

(1)证明　因为平面ABD⊥平面BCD，平面ABD∩平面BCD＝BD，BD⊥DC，DC平面BCD，

所以DC⊥平面ABD.

因为AB平面ABD，所以DC⊥AB，

又因为AD⊥AB，且DC∩AD＝D，

所以AB⊥平面ADC.

(2)解　由(1)知DC⊥平面ABD，所以∠DAC为AC与平面ABD所成角.

依题意得tan∠DAC＝＝，

因为AD＝1，所以CD＝，

设AB＝x(x>0)，则BD＝，

因为△ABD∽△DCB，所以＝，即，

解得x＝，故AB＝，BD＝.

过A作AOBD于O，则AO平面BDC，过O作OG//DC交BC于G，以O为坐标原点 OB，OG，OA分别为x.y.z轴非负半轴建立空间直角坐标系如图所示

面ABD法向量可取

DO=，OA=

D（,0,0） A（0,0，），，

，所以 ，

设面DAE法向量为则

取

又二面角B—AD—E是锐角，所以所求二面角的余弦值为。