题目内容
【题目】椭圆![]() 经过点
经过点![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,
,![]() ,
,![]() 点在椭圆上,且满足
点在椭圆上,且满足![]() 的
的![]() 点只有两个.
点只有两个.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 且不垂直于坐标轴的直线
且不垂直于坐标轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,在
两点,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 的角平分线是
的角平分线是![]() 轴?若存在求出
轴?若存在求出![]() ,若不存在,说明理由.
,若不存在,说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
(Ⅰ)由题得![]() 点为椭圆的上下顶点,得到a,b,c的方程组,解方程组即得椭圆的标准方程;(Ⅱ)设直线
点为椭圆的上下顶点,得到a,b,c的方程组,解方程组即得椭圆的标准方程;(Ⅱ)设直线![]() 的方程为
的方程为![]() ,联立直线和椭圆方程得到韦达定理,根据
,联立直线和椭圆方程得到韦达定理,根据![]() 得到
得到![]() . 所以存在点
. 所以存在点![]() ,使得
,使得![]() 的平分线是
的平分线是![]() 轴.
轴.
解:(I)由题设知![]() 点为椭圆的上下顶点,所以
点为椭圆的上下顶点,所以![]() ,b=c,
,b=c,![]() ,
,
故![]() ,
,![]() ,
,
故椭圆![]() 方程为
方程为![]() .
.
(Ⅱ)设直线![]() 的方程为
的方程为![]() ,联立
,联立
![]() 消
消![]() 得
得![]()
设![]() ,
,![]() 坐标为
坐标为![]() ,
,![]() 则有
则有
![]() ,
,![]() ,又
,又![]() ,
,![]()
假设在![]() 轴上存在这样的点
轴上存在这样的点![]() ,使得
,使得![]() 轴是
轴是![]() 的平分线,则有
的平分线,则有![]()
而![]()
![]()
![]()
![]()
将,![]() ,
,![]() 代入
代入![]()
有![]()
![]()
即![]()
因为![]() ,故
,故![]() . 所以存在点
. 所以存在点![]() ,使得
,使得![]() 的平分线是
的平分线是![]() 轴.
轴.

练习册系列答案
相关题目
【题目】现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了![]() 人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
月收入(单位百元) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
赞成人数 |
|
|
|
|
|
|
(1)由以上统计数据填下面![]() 列联表,并问是否有
列联表,并问是否有![]() 的把握认为“月收入以
的把握认为“月收入以![]() 元为分界点对“楼市限购令”的态度有差异;
元为分界点对“楼市限购令”的态度有差异;
月收入不低于 | 月收入低于 | 合计 | |
赞成 |
|
| ______________ |
不赞成 |
|
| ______________ |
合计 | ______________ | ______________ | ______________ |
(2)若对在![]() 、
、![]() 的被调查者中各随机选取两人进行追踪调查,记选中的
的被调查者中各随机选取两人进行追踪调查,记选中的![]() 人中不赞成“楼市限购令”的人数为
人中不赞成“楼市限购令”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: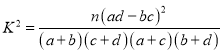 ,其中
,其中![]() .
.
参考值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

