题目内容
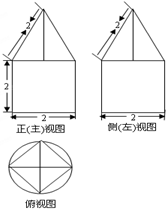
一空间几何体的三视图如图所示.
(1)求该几何体的体积;
(2)求表面积.

(1)求该几何体的体积;
(2)求表面积.
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:该空间几何体为一圆柱和一正四棱锥组成的,圆柱的底面半径为1,高为2.四棱锥的底面对角线长为圆的直径为2,高为
,分别计算体积,再相加即可.几何体的体积由圆柱的表面积与棱锥的侧面积减棱锥的底面积构成,进而可得答案.
| 3 |
解答:
解:该空间几何体为一圆柱和一四棱锥组成的,
圆柱的底面半径为1,高为2,体积为π×12×2=2π,
四棱锥的底面对角线长为2,高为
=
,
体积为
×(
×2×2)×
=
,
所以该几何体的体积为2π+
,
几何体的体积由圆柱的表面积与棱锥的侧面积减棱锥的底面积构成,
圆柱的表面积为:2π×1×(1+2)=6π,
棱锥的底面面积为:
×2×2=2,
棱锥的底面边长为:
,
棱锥的侧高为:
=
,
故棱锥的侧面积为:4×(
×
×
)=2
,
故几何体的表面积为:6π+2
-2.
圆柱的底面半径为1,高为2,体积为π×12×2=2π,
四棱锥的底面对角线长为2,高为
| 22-12 |
| 3 |
体积为
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
所以该几何体的体积为2π+
2
| ||
| 3 |
几何体的体积由圆柱的表面积与棱锥的侧面积减棱锥的底面积构成,
圆柱的表面积为:2π×1×(1+2)=6π,
棱锥的底面面积为:
| 1 |
| 2 |
棱锥的底面边长为:
| 2 |
棱锥的侧高为:
22-(
|
| ||
| 2 |
故棱锥的侧面积为:4×(
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 7 |
故几何体的表面积为:6π+2
| 7 |
点评:本题是基础题,考查三视图与几何体的关系,空间想象能力,逻辑思维能力,常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数f(x)的导函数图象如图所示,若△ABC为锐角三角形,则一定成立的是( )
已知函数f(x)的导函数图象如图所示,若△ABC为锐角三角形,则一定成立的是( )| A、f(cosA)<f(cosB) |
| B、f(sinA)<f(cosB) |
| C、f(sinA)>f(sinB) |
| D、f(sinA)>f(cosB) |
已知a=ln0.3,b=e0.3,c=0.3e(e为无理数,e≈2.71),则a,b,c的大小关系是( )
| A、a<b<c |
| B、c<a<b |
| C、a<c<b |
| D、b<c<a |
 已知函数f(x)=
已知函数f(x)=