题目内容
3.已知实数a、b满足0<a<1,0<b<1,求证:$\sqrt{{a}^{2}+{b}^{2}}$+$\sqrt{(a-1)^{2}+{b}^{2}}$+$\sqrt{{a}^{2}+(b-1)^{2}}$+$\sqrt{(a-1)^{2}+(b-1)^{2}}$≥2$\sqrt{2}$.分析 建立坐标系,正方形的边长为1,则O(0,0),A(1,0),B(1,1),C(0,1),正方形内取点D(a,b),a、b满足0<a<1,0<b<1,$\sqrt{{a}^{2}+{b}^{2}}$+$\sqrt{(a-1)^{2}+{b}^{2}}$+$\sqrt{{a}^{2}+(b-1)^{2}}$+$\sqrt{(a-1)^{2}+(b-1)^{2}}$表示OD+AD+CD+BD,利用OD+BD≥OB,AD+CD≥AC,即可证明结论.
解答 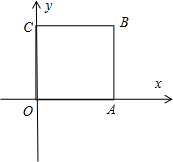 证明:建立如图所示的坐标系,正方形的边长为1,则O(0,0),A(1,0),B(1,1),C(0,1),正方形内取点D(a,b),a、b满足0<a<1,0<b<1,
证明:建立如图所示的坐标系,正方形的边长为1,则O(0,0),A(1,0),B(1,1),C(0,1),正方形内取点D(a,b),a、b满足0<a<1,0<b<1,
$\sqrt{{a}^{2}+{b}^{2}}$+$\sqrt{(a-1)^{2}+{b}^{2}}$+$\sqrt{{a}^{2}+(b-1)^{2}}$+$\sqrt{(a-1)^{2}+(b-1)^{2}}$表示OD+AD+CD+BD,利用OD+BD≥OB,AD+CD≥AC,
可得OD+AD+CD+BD≥OB+AC=2$\sqrt{2}$,
∴$\sqrt{{a}^{2}+{b}^{2}}$+$\sqrt{(a-1)^{2}+{b}^{2}}$+$\sqrt{{a}^{2}+(b-1)^{2}}$+$\sqrt{(a-1)^{2}+(b-1)^{2}}$≥2$\sqrt{2}$.
点评 本题考查不等式的证明,考查构造法的运用,正确利用几何意义是关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
18.已知f(x)是定义在R上的奇函数,若对于x≥0,都有f(x+2)=f(x),且当x∈[0,2)时,f(x)=ex-1,则f(-2014)+f(2015)=( )
| A. | 1-e | B. | e-1 | C. | -1-e | D. | e+1 |
12.已知O为坐标原点,A(0,1),B(-3,4),C在角∠AOB的平分线上,|$\overrightarrow{OC}$|=2,C坐标为( )
| A. | ($\frac{\sqrt{10}}{5}$,$\frac{3\sqrt{10}}{5}$) | B. | (-$\frac{\sqrt{10}}{5}$,-$\frac{3\sqrt{10}}{5}$) | C. | ($\frac{\sqrt{10}}{5}$,-$\frac{3\sqrt{10}}{5}$) | D. | (-$\frac{\sqrt{10}}{5}$,$\frac{3\sqrt{10}}{5}$) |