题目内容
8.若函数f(x)=2sin2ωx+sin2ωx-1(x∈R)满足f(α)=-$\sqrt{2}$,f(β)=0且|α-β|的最小值为$\frac{3π}{4}$,则正数ω的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{5}$ |
分析 由条件利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性,求得正数ω的值.
解答 解:∵函数f(x)=2sin2ωx+sin2ωx-1=sin2ωx-cos2ωx=$\sqrt{2}$sin(2ωx-$\frac{π}{4}$)(x∈R),
满足f(α)=-$\sqrt{2}$,f(β)=0,且|α-β|的最小值为$\frac{3π}{4}$,故函数f(x)的最小正周期为4•$\frac{3π}{4}$=3π=$\frac{2π}{2ω}$,
则正数ω=$\frac{1}{3}$,
故选:A.
点评 本题主要考查三角函数的恒等变换,正弦函数的周期性,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.“|x-1|+|x+2|≤5”是“-3≤x≤2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.已知函数f(x)=$\left\{{\begin{array}{l}{f({x+2}),x<3}\\{{{({\frac{1}{2}})}^x},x≥3}\end{array}}$,则f(-4)=( )
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
16.已知数列{an},若点(n,an)(n∈N*)在经过点(10,6)的定直线上,则数列{an}的前19项和S19的值为( )
| A. | 190 | B. | 114 | C. | 60 | D. | 120 |
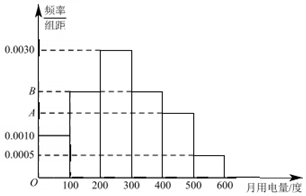 某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费.超过200度但不超过400度的部分按0.8 元/度收费,超过400度的部分按1.0 元/度收费.
某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费.超过200度但不超过400度的部分按0.8 元/度收费,超过400度的部分按1.0 元/度收费. 用黑白两种颜色随机地染如图所示表格中6个格子,每个格子染一种颜色,则有64个不同的染色方法,出现从左至右数,不管数到哪个格子,总有黑色格子不少于白色格子的概率为$\frac{5}{16}$.
用黑白两种颜色随机地染如图所示表格中6个格子,每个格子染一种颜色,则有64个不同的染色方法,出现从左至右数,不管数到哪个格子,总有黑色格子不少于白色格子的概率为$\frac{5}{16}$.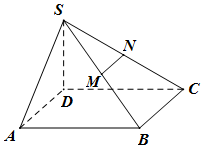 已知四棱锥S-ABCD的底面为平行四边形,且SD⊥面ABCD,AB=2AD=2SD,∠DCB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.
已知四棱锥S-ABCD的底面为平行四边形,且SD⊥面ABCD,AB=2AD=2SD,∠DCB=60°,M、N分别为SB、SC中点,过MN作平面MNPQ分别与线段CD、AB相交于点P、Q.