题目内容
6. 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,PO=1,M为PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,PO=1,M为PD的中点.(Ⅰ)证明:PB∥平面ACM;
(Ⅱ)设直线AM与平面ABCD所成的角为α,二面角M-AC-B的大小为β,求sinαcosβ的值.
分析 (Ⅰ)连结OM,推导出OM∥PB,由此能证明PB∥平面ACM.
(2)取DO的中点N,连结MN,AN,则MN∥PO,推导出∠MAN=α为所求的直线AM与平面ABCD所成的角,从而求出sinα=$\frac{MN}{AM}=\frac{2}{3}$,取AO的中点R,连结NR,MR,则∠MRN为二面角M-AC-B的补角,即为π-β.从而得到cos(π-β)=-cosβ=$\frac{\sqrt{2}}{2}$,由此能求出sinαcosβ.
解答 证明:(Ⅰ)连结OM,在△PBD中,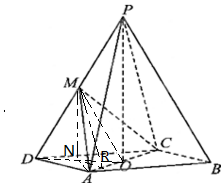
∵O为AC的中点,M为PD的中点.∴OM∥PB,
∵OM?平面ACM,PB?平面ACM,
∴PB∥平面ACM;(4分)
解:(2)取DO的中点N,连结MN,AN,则MN∥PO,
∵PO⊥平面ABCD,∴MN⊥平面ABCD,
∴∠MAN=α为所求的直线AM与平面ABCD所成的角.
∵MN=$\frac{1}{2}$PO=$\frac{1}{2}$,
在Rt△ADO中,∵DO=$\sqrt{{1}^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{5}}{2}$,AN=$\frac{1}{2}$DO=$\frac{\sqrt{5}}{4}$,
在Rt△AMN中,AM=$\sqrt{(\frac{\sqrt{5}}{4})^{2}+(\frac{1}{2})^{2}}$=$\frac{3}{4}$,
∴sinα=$\frac{MN}{AM}=\frac{2}{3}$,(8分)
取AO的中点R,连结NR,MR,
∵NR∥AD,∴NR⊥OA,MN⊥平面ABCD,
由三垂线定理知MR⊥AO,故∠MRN为二面角M-AC-B的补角,即为π-β.
∵NR=$\frac{1}{2}$,MN=$\frac{1}{2}$,∴cos(π-β)=-cosβ=$\frac{\sqrt{2}}{2}$,(11分)
∴sinαcosβ=$\frac{2}{3}×(-\frac{\sqrt{2}}{2})$=-$\frac{\sqrt{2}}{3}$.(12分)
点评 本题考查线面平行的证明,考查线面角的正弦值和二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | $\frac{18}{35}$ | B. | $\frac{15}{35}$ | C. | $\frac{12}{35}$ | D. | $\frac{9}{35}$ |
| A. | b<a<c | B. | a<b<c | C. | b<c<a | D. | c<a<b |
| A. | m>1 | B. | $m>\frac{1}{2}$ | C. | m>2 | D. | m≥1 |
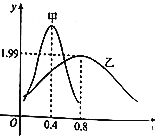 甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ12)及N(μ2,σ22),其正态分布的密度曲线如图所示,则下列说法错误的是( )
甲、乙两类水果的质量(单位:kg)分别服从正态分布N(μ1,σ12)及N(μ2,σ22),其正态分布的密度曲线如图所示,则下列说法错误的是( )| A. | 乙类水果的质量服从的正态分布的参数σ2=1.99 | |
| B. | 甲类水果的质量比乙类水果的质量更集中 | |
| C. | 甲类水果的平均质量μ1=0.4kg | |
| D. | 甲类水果的平均质量比乙类水果的平均质量小 |
| A. | {x|x=2kπ+$\frac{4π}{3}$,k∈Z} | B. | {x|x=2kπ+$\frac{π}{3}$,k∈Z} | C. | {$\frac{4π}{3}$,$\frac{π}{3}$} | D. | {x|x=kπ+$\frac{π}{3}$,k∈Z} |