题目内容
函数y=f(x)在[-1,2]上单调递减,且f(2a+1)>f(2-a),则a的取值范围为________.
0≤a<
分析:利用单调性f(2a+1)>f(2-a)可化为2a+1<2-a,再由定义域可得 ,取各不等式的交集即得a的取值范围.
,取各不等式的交集即得a的取值范围.
解答:因为f(x)单调递减,且f(2a+1)>f(2-a),
所以2a+1<2-a,解得a< ①
①
又f(x)的定义域为[-1,2],
所以 ,解得0≤a≤
,解得0≤a≤ ②,
②,
联立①②解得0≤a .
.
故答案为:0≤a< .
.
点评:本题考查函数单调性的性质,考查抽象不等式的求解,考查学生的转化能.

分析:利用单调性f(2a+1)>f(2-a)可化为2a+1<2-a,再由定义域可得
 ,取各不等式的交集即得a的取值范围.
,取各不等式的交集即得a的取值范围.解答:因为f(x)单调递减,且f(2a+1)>f(2-a),
所以2a+1<2-a,解得a<
 ①
①又f(x)的定义域为[-1,2],
所以
 ,解得0≤a≤
,解得0≤a≤ ②,
②,联立①②解得0≤a
 .
.故答案为:0≤a<
 .
.点评:本题考查函数单调性的性质,考查抽象不等式的求解,考查学生的转化能.

练习册系列答案
相关题目
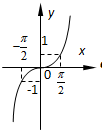 已知函数y=f(x)的图象如图,则函数
已知函数y=f(x)的图象如图,则函数