题目内容
9．在正方体ABCD-A1B1C1D1中，E、F分别为AB、AD的中点，则EF与B1C所成的角等于（ ）| A． | 45° | B． | 30° | C． | 90° | D． | 60° |
分析 以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，利用向量法能求出EF与B1C所成的角．
解答 
解：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，
设正方体ABCD-A1B1C1D1的棱长为2，
则E（2，1，0），F（1，0，0），B1（2，2，2），C（0，2，0），
∴$\overrightarrow{EF}$=（-1，-1，0），$\overrightarrow{{B}_{1}C}$=（-2，0，-2），
∴COS＜$\overrightarrow{EF}，\overrightarrow{{B}_{1}C}$＞=$\frac{2}{\sqrt{2}•\sqrt{8}}$=$\frac{1}{2}$，
∴则EF与B1C所成的角等于60°．
故选：D．
点评 本题考查异面直线所成角的求法，是基础题，解题时要认真审题，注意向量法的合理运用．
练习册系列答案
相关题目
4．
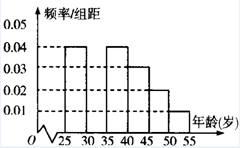某班同学在暑假期间进行社会实践活动，从本地[25，55]岁的人群中随机抽取n人进行
了一次有关“房地产投资”的调查，得到如下统计数据和频率分布直方图：
（Ⅰ）求n，a，p的值；
（Ⅱ）从年龄在[40，50）岁的“房地产投资”人群中采取分层抽样法抽取9人参加投资管理学习活动，并从中选取3人作为代表发言，记选取的3名代表中年龄在
[40，45）岁的人数为X，求X的分布列和数学期望．
某班同学在暑假期间进行社会实践活动，从本地[25，55]岁的人群中随机抽取n人进行了一次有关“房地产投资”的调查，得到如下统计数据和频率分布直方图：
| 组数 | 分组 | 房地产投资的人数 | 占本组的频率 |
| 第一组 | [25，30） | 120 | 0.6 |
| 第二组 | [30，35） | 195 | P |
| 第三组 | [35，40） | 100 | 0.5 |
| 第四组 | [40，45） | a | 0.4 |
| 第五组 | [45，50） | 30 | 0.3 |
| 第六组 | [50，55] | 15 | 0.3 |
（Ⅱ）从年龄在[40，50）岁的“房地产投资”人群中采取分层抽样法抽取9人参加投资管理学习活动，并从中选取3人作为代表发言，记选取的3名代表中年龄在
[40，45）岁的人数为X，求X的分布列和数学期望．
19．若输入8，则图程序执行后输出的结果是（ ）
| A． | 0.2 | B． | 0.7 | C． | 0.8 | D． | 1 |