题目内容
13.已知函数f(x)=ax+$\frac{a-1}{x}$-2a+1(a>0).(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)≥lnx在[1,+∞)上恒成立,求实数a的取值范围;
(Ⅲ)证明:$\sum_{k=2}^n{ln\frac{k-1}{k+1}}>\frac{{2-n-{n^2}}}{{\sqrt{2n(n+1)}}}$.
分析 (Ⅰ)求出f(x)的定义域,以及导函数,根据导函数的正负与增减性的关系判断即可确定出f(x)的单调区间;
(Ⅱ)令g(x)=ax+$\frac{a-1}{x}$-2a+1-lnx,x∈[1,+∞),求出g(1)的值以及导函数,根据导函数的正负与增减性的关系确定出f(x)≥lnx在[1,+∞)上恒成立时实数a的取值范围即可;
(Ⅲ)令a=$\frac{1}{2}$,根据第二问的结论列出关系式,进而可得当lnx2<x-$\frac{1}{x}$(x>1)(*),所证不等式等价于ln$\frac{2}{n(n+1)}$>$\frac{2-n-{n}^{2}}{\sqrt{2n(n+1)}}$,令x=$\sqrt{\frac{n(n+1)}{2}}$>1(n>2),代入不等式(*),整理即可得证.
解答 (Ⅰ)解:f(x)的定义域为{x|x≠0},f′(x)=a-$\frac{a-1}{{x}^{2}}$=$\frac{a{x}^{2}+1-a}{{x}^{2}}$(a>0),
当0<a≤1时,f'(x)>0恒成立,此时,f(x)在(-∞,0),(0,+∞)上是增函数;
当a≥1时,令f'(x)=0得:x1=-$\sqrt{\frac{a-1}{a}}$,x2=$\sqrt{\frac{a-1}{a}}$,
列表如下:
| x | (-∞,x1) | (x1,0) | (0,x2) | (x2,+∞) |
| f'(x) | + | _ | _ | + |
| f(x) | 增 | 减 | 减 | 增 |
(Ⅱ)解:g(x)=ax+$\frac{a-1}{x}$-2a+1-lnx,x∈[1,+∞),
则g(1)=0,g′(x)=a-$\frac{a-1}{x^2}$-$\frac{1}{x}$=$\frac{{a{x^2}-x-(a-1)}}{x^2}$=$\frac{{a(x-1)(x-\frac{1-a}{a})}}{x^2}$,
(i)当0<a<$\frac{1}{2}$时,$\frac{1-a}{a}$>1,
若1<x<$\frac{1-a}{a}$,则g′(x)<0,g(x)是减函数,
∴g(x)<g(1)=0,即f(x)>lnx,
故f(x)≥lnx在[1,+∞)上不恒成立;
(ii)当a≥$\frac{1}{2}$时,$\frac{1-a}{a}$≤1,
若x>1,则g′(x)>0,g(x)是增函数,
∴g(x)>g(1)=0,即f(x)>lnx,
故当x≥1时,f(x)≥lnx,
综上所述,所求a的取值范围是[$\frac{1}{2}$,+∞);
(Ⅲ)证明:在(2)中,令a=$\frac{1}{2}$,可得不等式:lnx≤$\frac{1}{2}$(x-$\frac{1}{x}$)(x≥1)(当且仅当x=1时等号成立),
进而可得当lnx2<x-$\frac{1}{x}$(x>1)(*),
$\sum_{k=2}^{n}$ln$\frac{k-1}{k+1}$>$\frac{2-n-{n}^{2}}{\sqrt{2n(n+1)}}$?ln$\frac{2}{n(n+1)}$>$\frac{2-n-{n}^{2}}{\sqrt{2n(n+1)}}$,
令x=$\sqrt{\frac{n(n+1)}{2}}$>1(n>2),代入不等式(*)得:ln$\frac{n(n+1)}{2}$<$\sqrt{\frac{n(n+1)}{2}}$-$\sqrt{\frac{2}{n(n+1)}}$=$\frac{n(n+1)}{\sqrt{2n(n+1)}}$-$\frac{2}{\sqrt{2n(n+1)}}$=$\frac{{n}^{2}+n-2}{\sqrt{2n(n+1)}}$,
则所证不等式成立.
点评 此题考查了利用导数求闭区间上函数的最值,以及利用导数研究函数的增减性,以及恒成立问题,熟练掌握导函数的性质与函数增减性的关系是解本题的关键.

练习册系列答案
相关题目
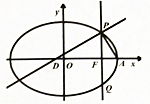 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{2}=1(a>0)$,点A,F分别为其右顶点和右焦点,过F作AF的垂线交椭圆C于P,Q两点,过P作AP的垂线交x轴于点D,若|DF|=$\frac{a+\sqrt{{a}^{2}-2}}{2}$,则椭圆C的长轴长为( )
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{2}=1(a>0)$,点A,F分别为其右顶点和右焦点,过F作AF的垂线交椭圆C于P,Q两点,过P作AP的垂线交x轴于点D,若|DF|=$\frac{a+\sqrt{{a}^{2}-2}}{2}$,则椭圆C的长轴长为( )