题目内容
5．在等差数列{an}中，a1=-2016，其前n项和为Sn，若$\frac{{{S_{20}}}}{20}-\frac{{{S_{18}}}}{18}$=2，则S2016的值等于-2016．分析 由已知条件利用等差数列的前n项和公式得到$\frac{20{a}_{1}+\frac{20×19}{2}d}{20}$-$\frac{18{a}_{1}+\frac{18×17}{2}d}{18}$=d=2，由此能求出S2016的值．
解答 解：在等差数列{an}中，
∵an=a1+（n-1）d，
${S}_{n}=n{a}_{1}+\frac{n（n-1）}{2}d$=n（${a}_{1}+\frac{n-1}{2}d$），
a1=-2016，其前n项和为Sn，$\frac{{{S_{20}}}}{20}-\frac{{{S_{18}}}}{18}$=2，
∴$\frac{20{a}_{1}+\frac{20×19}{2}d}{20}$-$\frac{18{a}_{1}+\frac{18×17}{2}d}{18}$=d=2，
∴S2016=2016a1+$\frac{2016×2015}{2}×2$=2016×（-2016）+2016×2015=-2016．
故答案为：-2016．
点评 本题考查等差数列的前2016项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
20．已知F1，F2分别为双曲线C：$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的左右焦点，过F1的直线l与双曲线C的左右两支分别交于A，B两点，若|AB|：|BF2|：|AF2|=4：3：5，则双曲线的离心率为（ ）
| A． | $\sqrt{13}$ | B． | $\sqrt{15}$ | C． | 2 | D． | $\sqrt{5}$ |
10．
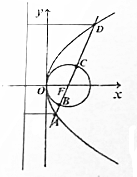如图，抛物线：y2=4mx（m＞0）和圆：x2+y2-2mx=0，直线l经过抛物线的焦点，依次交抛物线，圆于A，B，C，D四点，|AB|•|CD|=2，则m的值为（ ）
如图，抛物线：y2=4mx（m＞0）和圆：x2+y2-2mx=0，直线l经过抛物线的焦点，依次交抛物线，圆于A，B，C，D四点，|AB|•|CD|=2，则m的值为（ ）| A． | 2 | B． | $\sqrt{3}$ | C． | $\sqrt{2}$ | D． | 1 |
17．已知点A（-3，1，-4），则点A关于原点对称的点的坐标为（ ）
| A． | （-3，-1，4） | B． | （-3，-1，-4） | C． | （3，1，4） | D． | （3，-1，4） |