��Ŀ����
�趨��������[x1�� x2]�ϵĺ���y =f(x)��ͼ��ΪC��M��C�ϵ�����һ�㣬OΪ����ԭ�㣬������
=f(x)��ͼ��ΪC��M��C�ϵ�����һ�㣬OΪ����ԭ�㣬������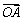 =
=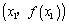 ��
��
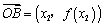 ��
��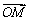 =(x��y)����ʵ��������x=�� x1+(1����) x2ʱ��������
=(x��y)����ʵ��������x=�� x1+(1����) x2ʱ��������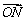 =��
=��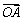 +(1����)
+(1����)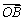 �����塰����y=f(x)������[x1��x2]�Ͽ��ڱ�k�����Խ��ơ���ָ��
�����塰����y=f(x)������[x1��x2]�Ͽ��ڱ�k�����Խ��ơ���ָ��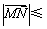 k�������������k��һ��ȷ����������
k�������������k��һ��ȷ����������
��1���躯�� f(x)=x2������[0��1]�Ͽ��ڱ�k�����Խ��ƣ���k��ȡֵ��Χ��
��2����֤������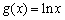 ������
������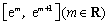 �Ͽ��ڱ�k=
�Ͽ��ڱ�k=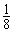 �����Խ��ƣ����ο����ݣ�e=2.718��ln(e��1)=
�����Խ��ƣ����ο����ݣ�e=2.718��ln(e��1)= 0.541��
0.541��
���⡿��1����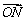 =��
=��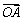 +(1����)
+(1����)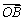 �õ�
�õ� =��
=�� ������B��N��A���㹲�ߣ� ����x=�� x1+(1����) x2������
������B��N��A���㹲�ߣ� ����x=�� x1+(1����) x2������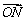 =��
=��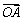 +(1����)
+(1����)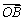 ����N��M�ĺ�������ͬ������ [0��1]�ϵĺ���y=x2��A(0��0)��B(1��1)��
����N��M�ĺ�������ͬ������ [0��1]�ϵĺ���y=x2��A(0��0)��B(1��1)��
���� ����
���� ������k��ȡֵ��Χ��
������k��ȡֵ��Χ�� ��
��
��2������ �ϵĺ���
�ϵĺ��� ��
��
A( )��B(
)��B( )�� ��ֱ��AB�ķ���
)�� ��ֱ��AB�ķ��� �� ��
�� �� ������
������ ������
������ �� �б����£�
�� �б����£�
| x | em | (em��em+1��em) | em+1��em | (em+1��em��em+1) | em+1 |
|
| + | 0 | �� | ||
|
| 0 | �� |
| �� | 0[ |

��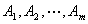 ����
����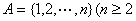 ��
��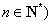 ���Ӽ�������������������
���Ӽ�������������������
��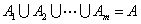 ���ڶ������
���ڶ������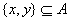 �����ٴ���һ��
�����ٴ���һ��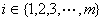 ��ʹ
��ʹ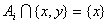 ��
��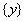 .
.
|
|
| �� |
|
|
|
| �� |
|
| �� | �� | �� | �� |
|
|
| �� |
|
��Ƽ�����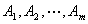 ��������
��������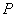 .��ͼ����
.��ͼ����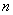 ��
��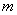 �����������������еĵ�
�����������������еĵ� �е�
�е� �е���Ϊ
�е���Ϊ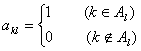 .
.
����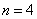 ʱ���ж����������������Ƿ��������
ʱ���ж����������������Ƿ��������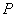 ��������뻭������Ӧ�ı������������˵�����ɣ�
��������뻭������Ӧ�ı������������˵�����ɣ�
������1��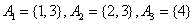 ��������2��
��������2��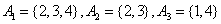 .
.
����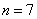 ʱ����������
ʱ����������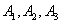 ��������
��������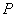 �����Ȼ�������Ӧ��
�����Ȼ�������Ӧ�� ��3�е�һ�������������˱���ֱ�д������
��3�е�һ�������������˱���ֱ�д������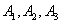 ������
������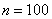 ʱ��������
ʱ��������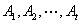 �Ǿ�������
�Ǿ�������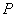 ���������ϸ�����С�ļ����飬��
���������ϸ�����С�ļ����飬�� ��ֵ��
��ֵ��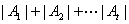 ����Сֵ.������
����Сֵ.������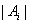 ��ʾ����
��ʾ����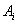 ����Ԫ�صĸ�����
����Ԫ�صĸ�����



 ���溯��
���溯�� ���������ڽ����ľ�����
���������ڽ����ľ����� ����
���� ����
���� ��ֵ.
��ֵ. ����
���� �����
����� ��һ���β����㣮�躯��
��һ���β����㣮�躯�� �뺯��
�뺯�� ������
������ Ϊ��Ȼ�����ĵ����������дβ�����֮��Ϊ
Ϊ��Ȼ�����ĵ����������дβ�����֮��Ϊ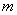 ����A��
����A�� B��
B�� C��
C�� D��
D��
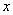 �ķ���
�ķ��� ֻ��һ��ʵ��������
ֻ��һ��ʵ��������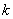 ��ȡֵ��ΧΪ�� ��
��ȡֵ��ΧΪ�� ��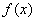 �Ķ�����ΪD�����������ʵ��k��ʹ������
�Ķ�����ΪD�����������ʵ��k��ʹ������ ������
������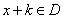 ����
����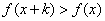 ���������ƺ���
���������ƺ���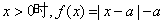 ������aΪ����������
������a����������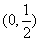 D��
D��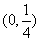

 ��ż��������
��ż��������








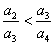 �� B��
�� B��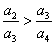 �� C��
�� C��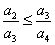 �� D��
�� D��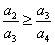 ��
�� 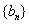 �ǵȱ����У�
�ǵȱ����У�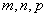 �ǻ�����ȵ���������������ȷ�Ľ��ۣ�
�ǻ�����ȵ���������������ȷ�Ľ��ۣ�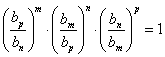 ������������ʣ���Ӧ�أ���
������������ʣ���Ӧ�أ���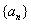 �ǵȲ����У�
�ǵȲ����У�