题目内容
10.在△ABC中,角A,B,C所对边分别为a,b,c,$\frac{sinA}{sinB+sinC}$=1-$\frac{a-b}{a-c}$.(1)若b=$\sqrt{3}$,求△ABC周长的取值范围;
(2)设$\overrightarrow{m}$=(sinA,1),$\overrightarrow{n}$=(6cosB,cos2A),求$\overrightarrow{m}$•$\overrightarrow{n}$的取值范围.
分析 (1)由$\frac{sinA}{sinB+sinC}$=1-$\frac{a-b}{a-c}$,利用正弦定理可得$\frac{a}{b+c}$=1-$\frac{a-b}{a-c}$,化简再利用余弦定理可得cosA=$\frac{1}{2}$,A∈(0,π),$A=\frac{π}{3}$.由正弦定理可得△ABC周长=a+$\sqrt{3}$+c=$\frac{3(1+cosB)}{sinB}$+2$\sqrt{3}$,令f(B)=$\frac{1+cosB}{sinB}$,则f(B)=$\frac{cosB-(-1)}{sinB-0}$表示点(0,-1)与点(sinB,cosB)连线的斜率,$B∈(0,\frac{2π}{3})$,可得f(B)>$\frac{\sqrt{3}}{3}$.即可得出.
(2)由(1)可得:A=$\frac{π}{3}$.利用数量积运算性质可得:$\overrightarrow{m}$•$\overrightarrow{n}$=6sinAcosB+cos2A=3$\sqrt{3}$cosB-$\frac{1}{2}$.由于B∈$(0,\frac{2π}{3})$,可得cosB∈$(-\frac{1}{2},1)$.即可得出.
解答 解:(1)∵$\frac{sinA}{sinB+sinC}$=1-$\frac{a-b}{a-c}$,∴$\frac{a}{b+c}$=1-$\frac{a-b}{a-c}$,化为:a2+c2-b2=ac,
∴cosA=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{ac}{2ac}$=$\frac{1}{2}$,A∈(0,π),
∴$A=\frac{π}{3}$.
由正弦定理可得:$\frac{a}{sin\frac{π}{3}}$=$\frac{\sqrt{3}}{sinB}$=$\frac{c}{sinC}$,
∴a=$\frac{3}{2sinB}$,c=$\frac{\sqrt{3}sinC}{sinB}$,
∴△ABC周长=a+$\sqrt{3}$+c=$\frac{3}{2sinB}$+$\sqrt{3}$+$\frac{\sqrt{3}sinC}{sinB}$=$\frac{3+2\sqrt{3}sin(\frac{2π}{3}-B)}{2sinB}$+$\sqrt{3}$=$\frac{3(1+cosB)}{sinB}$+2$\sqrt{3}$,
令f(B)=$\frac{1+cosB}{sinB}$,则f(B)=$\frac{cosB-(-1)}{sinB-0}$表示点(0,-1)与点(sinB,cosB)连线的斜率,$B∈(0,\frac{2π}{3})$,∴f(B)>$\frac{\sqrt{3}}{3}$.
∴△ABC周长的取值范围是$(3\sqrt{3},+∞)$.
(2)由(1)可得:A=$\frac{π}{3}$.
$\overrightarrow{m}$•$\overrightarrow{n}$=6sinAcosB+cos2A=$6sin\frac{π}{3}$cosB+$cos\frac{2π}{3}$=3$\sqrt{3}$cosB-$\frac{1}{2}$.
∵B∈$(0,\frac{2π}{3})$,∴cosB∈$(-\frac{1}{2},1)$.
∴$\overrightarrow{m}$•$\overrightarrow{n}$的取值范围是$(-\frac{3\sqrt{3}+1}{2},3\sqrt{3}-\frac{1}{2})$.
点评 本题考查了正弦定理余弦定理、和差化积、斜率计算公式、三角函数求值、数量积运算性质,考查了推理能力与计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| 速度区间 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) | [100,110) |
| 车辆数 | 1 | 4 | 10 | 15 | 12 | 6 | 2 |
(2)试估计在这段路上,汽车行驶速度的标准差.(注:为了计算方便,速度取每个区间的中点)
| A. | 2π | B. | π | C. | $\frac{3π}{2}$ | D. | $\frac{π}{2}$ |
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
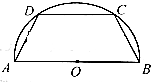 如图,有一块半径为R的半圆形钢板,计划将其剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.
如图,有一块半径为R的半圆形钢板,计划将其剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.