题目内容
17.若两平行直线3x-2y-1=0,6x+ay+c=0之间的距离为$\frac{{2\sqrt{13}}}{13}$,则c的值为2或-6.分析 由两直线平行得到x的系数之比等于y的系数之比不等于常数项之比求出a的值,然后把第二个方程等号两边都除以2后,利用两平行线间的距离公式表示出关于c的方程,求出方程的解即可得到c的值,把a和c的值代入即可求出所求式子的值.
解答 解:由题意得,$\frac{3}{6}$=$\frac{-2}{a}$≠$\frac{-1}{c}$,∴a=-4,c≠-2,
则6x+ay+c=0可化为3x-2y+$\frac{c}{2}$=0,
由两平行线间的距离公式,得$\frac{|\frac{c}{2}+1|}{\sqrt{13}}$=$\frac{2\sqrt{13}}{13}$,即|$\frac{c}{2}$+1|=2
解得c=2或-6,
故答案为:2或-6.
点评 此题考查学生掌握两直线平行的条件,灵活运用两平行线间的距离公式化简求值,是一道基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
8.一个正方体的表面涂上红色,在它的长、宽、高上等距离地各切三刀,则大正方形被分割成若干个小正方体,从小正方体中随机的取出一个,则这个小正方体各个面都没有涂红色的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{27}$ | D. | $\frac{1}{9}$ |
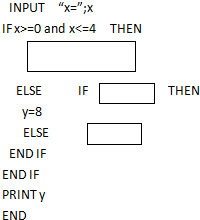 函数y=$\left\{\begin{array}{l}2x,0≤x≤4\\ 8,4<x≤8\\ 2(12-x),8<x≤12\end{array}$,填补方框内的内容完成函数的函数值的程序.
函数y=$\left\{\begin{array}{l}2x,0≤x≤4\\ 8,4<x≤8\\ 2(12-x),8<x≤12\end{array}$,填补方框内的内容完成函数的函数值的程序.