题目内容
已知数列{an}的前n项和Sn=n2，则a2等于（ ）
| A、1 | B、3 | C、4 | D、5 |
考点：数列递推式
专题：点列、递归数列与数学归纳法
分析：由于数列{an}的前n项和Sn=n2，n分别取1，2即可得出．
解答：
解：∵数列{an}的前n项和Sn=n2，
∴a1=S1=1，a1+a2=S2=22，
解得a2=3．
故选：B．
∴a1=S1=1，a1+a2=S2=22，
解得a2=3．
故选：B．
点评：本题考查了数列的递推式、前n项和，属于基础题．
练习册系列答案
相关题目
用反证法证明命题“设a，b为实数，则方程x2+ax+b=0至少有一个实根”时，要做的假设是（ ）
| A、方程x2+ax+b=0没有实根 |
| B、方程x2+ax+b=0至多有一个实根 |
| C、方程x2+ax+b=0至多有两个实根 |
| D、方程x2+ax+b=0恰好有两个实根 |
已知三条直线m、n、l，三个平面α、β、γ，下列四个命题中，正确的是（ ）
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
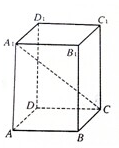如图所示，四棱柱ABCD-A1B1C1D1中，底面ABCD为正方形，高A1A=3，体积为24，则对角线A1C为