题目内容
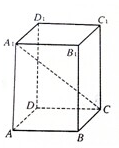 如图所示,四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,高A1A=3,体积为24,则对角线A1C为
如图所示,四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,高A1A=3,体积为24,则对角线A1C为考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:利用几何体的体积求出底面面积,求出底面边长,然后求解对角线A1C即可.
解答:
解:四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,高A1A=3,体积为24,
所以底面面积为:8,
底面边长为:2
.
对角线A1C=
=5.
故答案为:5.
所以底面面积为:8,
底面边长为:2
| 2 |
对角线A1C=
32+(2
|
故答案为:5.
点评:本题考查空间想象能力,几何体的体积与几何体中距离直接的关系式的应用,考查计算能力.

练习册系列答案
相关题目
如果4sin
+3cos
=0,那么角θ的终边所在的象限是( )
| θ |
| 2 |
| θ |
| 2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知数列{an}的前n项和Sn=n2,则a2等于( )
| A、1 | B、3 | C、4 | D、5 |
已知动点M与F(1,0)的距离比它到直线l:x+3=0的距离小2,设M的轨迹为G,正项数列{an}满足a1=2,且(an,
)在曲线G上,则数列{an}的通项公式为( )
| 2an+1 |
| A、an=2n |
| B、an=2n-1 |
| C、an=2n+1 |
| D、an=2-1 |
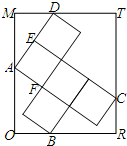 如图矩形ORTM内放置5个大小相同的正方形,其中A、B、C、D都在矩形的边上,若向量
如图矩形ORTM内放置5个大小相同的正方形,其中A、B、C、D都在矩形的边上,若向量