题目内容
已知函数g(x)=ax2-4ax+b(a>0)在区间[0,1]上有最大值1和最小值-2,设f(x)=
.
(Ⅰ)求a,b的值;
(Ⅱ)判断函数f(x)在(1,+∞)上的单调性,并证明你的结论;
(Ⅲ)若不等式f(2x)-k•2x≥0在x∈[-2,2]上有解,求实数k的取值范围.
| g(x) |
| x |
(Ⅰ)求a,b的值;
(Ⅱ)判断函数f(x)在(1,+∞)上的单调性,并证明你的结论;
(Ⅲ)若不等式f(2x)-k•2x≥0在x∈[-2,2]上有解,求实数k的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(Ⅰ)根据函数g(x)=ax2-4ax+b(a>0)在区间[0,1]上为减函数,且有最大值1和最小值-2,故可建立方程组,从而可求a、b的值;
(Ⅱ)利用导数判断并证明f(x)在区间(1,+∞)上的单调递增.
(Ⅲ)不等式f(2x)-k•2x≥0可化为:2x+
-4-k•2x≥0,即k≤1+(
)2-4•(
) ,利用换元法,结合二次函数的图象和性质,求出1+(
)2-4•(
) 的最小值,可得答案.
(Ⅱ)利用导数判断并证明f(x)在区间(1,+∞)上的单调递增.
(Ⅲ)不等式f(2x)-k•2x≥0可化为:2x+
| 1 |
| 2x |
| 1 |
| 2x |
| 1 |
| 2x |
| 1 |
| 2x |
| 1 |
| 2x |
解答:
解:(Ⅰ)g(x)=ax2-4ax+b(a>0)的图象是开口朝上,且以直线x=2为对称轴的抛物线,
故函数g(x)=ax2-4ax+b(a>0)在区间[0,1]上为减函数,
∵函数g(x)=ax2-4ax+b(a>0)在区间[0,1]上有最大值1和最小值-2,
∴
解得a=1,b=1;
(Ⅱ)由(Ⅰ)得:g(x)=x2-4x+1,f(x)=
=x+
-4,
∴f′(x)=1-
,
∵x∈(1,+∞),
∴f′(x)>0,
∴f(x)在区间(1,+∞)上的单调递增.
(Ⅲ)不等式f(2x)-k•2x≥0可化为:2x+
-4-k•2x≥0,
即k≤1+(
)2-4•(
) ,
令t=
,
∵x∈[-2,2],
∴t∈[
,4],
令h(t)=t2-4t+1,t∈[
,4],
∴h(t)∈[-3,1],
∴k≤1.
故所以k的取值范围是k≤1
故函数g(x)=ax2-4ax+b(a>0)在区间[0,1]上为减函数,
∵函数g(x)=ax2-4ax+b(a>0)在区间[0,1]上有最大值1和最小值-2,
∴
|
解得a=1,b=1;
(Ⅱ)由(Ⅰ)得:g(x)=x2-4x+1,f(x)=
| g(x) |
| x |
| 1 |
| x |
∴f′(x)=1-
| 1 |
| x2 |
∵x∈(1,+∞),
∴f′(x)>0,
∴f(x)在区间(1,+∞)上的单调递增.
(Ⅲ)不等式f(2x)-k•2x≥0可化为:2x+
| 1 |
| 2x |
即k≤1+(
| 1 |
| 2x |
| 1 |
| 2x |
令t=
| 1 |
| 2x |
∵x∈[-2,2],
∴t∈[
| 1 |
| 4 |
令h(t)=t2-4t+1,t∈[
| 1 |
| 4 |
∴h(t)∈[-3,1],
∴k≤1.
故所以k的取值范围是k≤1
点评:本题考查了恒成立问题,考查了二次函数的性质,训练了利用二次函数的单调性求最值,考查了数学转化思想方法,解答此题的关键在于把不等式在闭区间上有解转化为分离变量后的参数k小于等于函数在闭区间上的最大值,是学生难以想到的地方,是难题.

练习册系列答案
相关题目
已知平面点集M={(x,y)
},平面点集{(x,y)|x2+y2≤1},在集合M中任取一点P,则点P落在集合N中的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知抛物线y2=4x的焦点为F,过点P(2,0)的直线交抛物线于A,B两点,直线AF,BF分别与抛物线交于点C,D设直线AB,CD的斜率分别为k1,k2,则
等于( )
| k1 |
| k2 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
已知数列{an}的前n项和Sn=n2,则a2等于( )
| A、1 | B、3 | C、4 | D、5 |
已知动点M与F(1,0)的距离比它到直线l:x+3=0的距离小2,设M的轨迹为G,正项数列{an}满足a1=2,且(an,
)在曲线G上,则数列{an}的通项公式为( )
| 2an+1 |
| A、an=2n |
| B、an=2n-1 |
| C、an=2n+1 |
| D、an=2-1 |
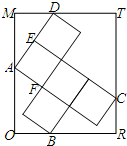 如图矩形ORTM内放置5个大小相同的正方形,其中A、B、C、D都在矩形的边上,若向量
如图矩形ORTM内放置5个大小相同的正方形,其中A、B、C、D都在矩形的边上,若向量